题目内容

函数f（x）=xsinx+cosx+1（x∈[0，π]的最大值为

A.
$数学公式$
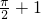
B.
2
C.
1
D.
0

A
分析：欲求函数f（x）=xsinx+cosx+1（x∈[0，π]的最大值，只需利用导数研究该函数在[0，π]上的单调性，从而可求出最值．
解答：∵f'（x）=xcosx
∴当 $\text{[math]}$ 时，f′（x）＞0，f（x）为增函数；
当 $\text{[math]}$ 时，，f′（x）＜0，f（x）为减函数，
∴ $\text{[math]}$ ．
故选A．
点评：本题主要考查了利用导数研究函数的单调性，以及利用导数求闭区间上函数的最值，同时考查了计算能力，属于基础题．

练习册系列答案

学业测评一卷通小学升学试题汇编系列答案

小学单元综合练习与检测系列答案

实验探究报告练习册系列答案

单元学习体验与评价系列答案

黄冈小状元小学升学考试冲刺复习卷系列答案

毕业总复习冲刺卷系列答案

学习指导系列答案

随堂同步练习系列答案

数学奥赛天天练系列答案

数学口算每天一练系列答案

相关题目

已知函数f（x）=xsinx，若x₁、x2∈[-

]且f（x₁）＜f（x₂），则下列不等式中正确的是（　　）

B、x₁＜x₂

C、x₁+x₂＜0

D、x₁²＜x₂²

某同学对函数f（x）=xsinx进行研究后，得出以下结论：
①函数y=f（x）的图象是轴对称图形；
②对任意实数x，|f（x）|≤|x|均成立；
③函数y=f（x）的图象与直线y=x有无穷多个公共点，且任意相邻两点的距离相等；
④当常数k满足|k|＞1时，函数y=f（x）的图象与直线y=kx有且仅有一个公共点．
其中所有正确结论的序号是（　　）

给出以下五个命题，其中所有正确命题的序号为

的最小值为l+2

；
②已知函数f （x）=|x²-2|，若f （a）=f （b），且0＜a＜b，则动点P（a，b）到直线4x+3y-15=0的距离的最小值为1；
③命题“函数f（x）=xsinx+1，当x₁，x₂∈[-

]，且|x₁|＞|x₂|时，有f （x₁）＞f（x₂）”是真命题；
④“a=

dx”是函数“y=cos²（ax）-sin²（ax）的最小正周期为4”的充要条件；
⑤已知等差数列{a_n}的前n项和为Sn，

为不共线向量，又

，则S₂₀₁₂=2013．

（2012•江西模拟）设函数f（x）=xsinx（x∈R）则f（log

）的大小关系为

（用“＜”连接）

给出以下三个命题，其中所有正确命题的序号为

均为单位向量，若|

|＞1，则θ∈[0，

)
②函数f （x）=xsinx+l，当x₁，x₂∈[-

]，且|x₁|＞|x₂|时，有f（x₁）＞f（x₂），
③已知函数f （x）=|x²-2|，若f （a）=f （b），且0＜a＜b，则动点P（a，b）到直线4x+3y-15=0的距离的最小值为1．