题目内容
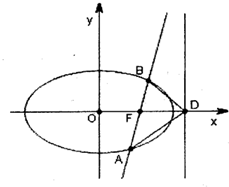 如图:椭圆
如图:椭圆| x2 |
| 2 |
| 2 |
| 3 |
分析:设直线AB的方程为x=ty+1,A(x1,y1),B(x2,y2),由
,得(t2+2)y2+2ty-1=0,由此能求出直线AB的方程.
|
解答:解:易得椭圆右焦点F的坐标(1,0),
点D的坐标为(2,0),
故|FD|=1.
显示直线AB与x轴不重合,
故设直线AB的方程为x=ty+1,
A(x1,y1),B(x2,y2),
由
,得(t2+2)y2+2ty-1=0
于是|y1-y2|=
=
所以S△ABD=
•|FD|•|y1-y2|=
=
,
整理得2t4-t2-1=0,
解得t2=1或t2=-
(舍去),
故t=1或t=-1.
所以直线AB的方程为x-y-1=0或x+y-1=0.
点D的坐标为(2,0),
故|FD|=1.
显示直线AB与x轴不重合,
故设直线AB的方程为x=ty+1,
A(x1,y1),B(x2,y2),
由
|
于是|y1-y2|=
| ||
| |t2+2| |
2
| ||
| t2+2 |
所以S△ABD=
| 1 |
| 2 |
| ||
| t2+2 |
| 2 |
| 3 |
整理得2t4-t2-1=0,
解得t2=1或t2=-
| 1 |
| 2 |
故t=1或t=-1.
所以直线AB的方程为x-y-1=0或x+y-1=0.
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
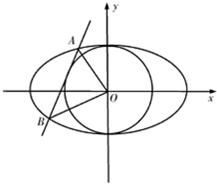 如图所示,已知圆O:x2+y2=1,直线l:y=kx+b(b>0)是圆的一条切线,且l与椭圆
如图所示,已知圆O:x2+y2=1,直线l:y=kx+b(b>0)是圆的一条切线,且l与椭圆 如图所示,已知圆O:x2+y2=1,直线l:y=kx+b(k>0,b>0)是圆的一条切线,且l与椭圆
如图所示,已知圆O:x2+y2=1,直线l:y=kx+b(k>0,b>0)是圆的一条切线,且l与椭圆 已知圆O:
已知圆O: