题目内容
8．过点A（-3，-4）作椭圆$\frac{{x}^{2}}{4}$+y2=1的切线l，求直线l的方程．分析 设切线l的方程为：y+4=k（x+3），与椭圆方程联立化为（1+4k2）x2+（24k2-32k）x+36k2-96k+60=0，利用△=0解出k即可．
解答 解：由题意可知切线l的斜率存在，设切线l的方程为：y+4=k（x+3），
化为y=kx+3k-4，
联立$\left\{\begin{array}{l}{y=kx+3k-4}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$，
化为（1+4k2）x2+（24k2-32k）x+36k2-96k+60=0，
∵△=（24k2-32k）2-4（1+4k2）（36k2-96k+60）=0，
化为：5k2-24k+15=0，解得k=$\frac{12±\sqrt{69}}{5}$．
∴直线l的方程为$y+4=\frac{12±\sqrt{69}}{5}（x+3）$．
点评 本题考查了直线与椭圆相切转化为方程联立可得△=0，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
16．在平面直角坐标系xOy中，椭圆$\frac{x{\;}^{2}}{a{\;}^{2}}$+$\frac{y{\;}^{2}}{b{\;}^{2}}$=1（a＞b＞0）内接四边形ABCD（点A、B、C、D在椭圆上）的对角线AC、BD相交于P（$\frac{1}{b{\;}^{2}}$，$\frac{1}{a{\;}^{2}}$），且$\overrightarrow{AP}$=λ$\overrightarrow{PC}$，$\overrightarrow{BP}$=λ$\overrightarrow{PD}$，则直线AB的斜率为（ ）
| A． | $\frac{-a{\;}^{2}-c{\;}^{2}}{c{\;}^{2}}$ | B． | $\frac{c（λ-1）}{a}$ | C． | -1 | D． | -2 |
3．为减少汽车尾气排放，提高空气质量，各地纷纷推出汽车尾号限行措施，为做好此项工作，某市交支队对市区各交通枢纽进行调查统计，表中列出了某交通路口单位时间内通过的1000辆汽车的车牌尾号记录：
由于某些数据缺失，表中以英文字母作标记，请根据图表提供的信息计算：
（Ⅰ）若采用分层抽样的方法从这1000辆汽车中抽取20辆，了解驾驶员对尾号限行的建议，应分别从一、二、三、四组中各抽取多少辆？
（Ⅱ）以频率代替概率，在此路口随机抽取4辆汽车，奖励汽车用品，用ξ表示车尾号在第二组的汽车数目，求ξ的分布列和数学期望．
| 组名 | 尾号 | 频数 | 频率 |
| 第一组 | 0、1、4 | 200 | 0.2 |
| 第二组 | 3、6 | 250 | 0.25 |
| 第三组 | 2、5、7 | a | b |
| 第四组 | 8、9 | e | 0.3 |
（Ⅰ）若采用分层抽样的方法从这1000辆汽车中抽取20辆，了解驾驶员对尾号限行的建议，应分别从一、二、三、四组中各抽取多少辆？
（Ⅱ）以频率代替概率，在此路口随机抽取4辆汽车，奖励汽车用品，用ξ表示车尾号在第二组的汽车数目，求ξ的分布列和数学期望．
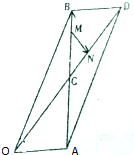如图，平行四边形OADB的对角线OD、AB相交于点C，线段BC上有一点M满足BC=3BM，线段CD上有一点N满足CD=3CN，设|$\overrightarrow{OA}$|=2，|$\overrightarrow{OB}$|=6，∠AOB=60°．
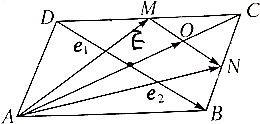已知在?ABCD中，M、N分别是DC、BC的中点，若$\overrightarrow{AM}$=$\overrightarrow{{e}_{1}}$，$\overrightarrow{AN}$=$\overrightarrow{{e}_{2}}$，试用$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$表示$\overrightarrow{DB}$、$\overrightarrow{AO}$．