题目内容
设函数f(x)=(x-1)2+mlnx,其中m为常数.
(1)当 在定义域上的单调性;
在定义域上的单调性;
(2)若函数f(x)有极值点,求实数m的取值范围及f(x)的极值点.
(3)当 .
.
解:(1)函数f(x)=(x-1)2+mlnx,可得函数的定义域为(0,+∞)
f′(x)=2(x+1)+ =
= =
= (x>0)
(x>0)
当m 时,可知f′(x)>0对任意x∈(0,+∞)恒成立,
时,可知f′(x)>0对任意x∈(0,+∞)恒成立,
∴函数f(x)在(0,+∞)上是单调递增函数.
(2)由(1)知,当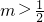 时,函数f(x)在(0,+∞)上是单调增函数,没有极值点.
时,函数f(x)在(0,+∞)上是单调增函数,没有极值点.
当 时,
时, ,函数f(x)在(0,+∞)上是单调增函数,没有极值点.
,函数f(x)在(0,+∞)上是单调增函数,没有极值点.
当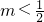 时,令f'(x)=0得,
时,令f'(x)=0得, ,
, …(6分)
…(6分)
①当m≤0时, ,则
,则 ,
,
列表:
由此看出,当m≤0时,f(x)有唯一极小值点 .…(8分)
.…(8分)
②当 时,0<x1<x2<1,
时,0<x1<x2<1,
列表:
由此看出,当 时,f(x)有极小值点
时,f(x)有极小值点 和极大值点
和极大值点 .
.
综上,当m≤0时,f(x)有唯一极小值点 ,
,
当 时,f(x)有极小值点
时,f(x)有极小值点 和极大值点
和极大值点 .…(10分)
.…(10分)
(3)由(2)知,m=-1时,函数f(x)=(x-1)2-lnx,
此时,函数f(x)有唯一极小值点 ,
,
当 时,f'(x)<0,f(x)在
时,f'(x)<0,f(x)在 上是减函数,
上是减函数,
∵n≥3时, ,
,
∴ ,即
,即
∴n≥3时, .
.
令函数h(x)=(x-1)-lnx(x>0),则
当x>1时,h′(x)>0,h(x)在(1,+∞)上是增函数,
∵n≥3时,1 ,∴
,∴ f(1),即
f(1),即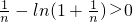
∴n≥3时,ln(n+1)-lnn
综上,当n≥3,n∈N时,不等式 恒成立.
恒成立.
分析:(1)求导数,通过m ,x>0,可判导数为正,可推f(x)在(0,+∞)上是增函数;
,x>0,可判导数为正,可推f(x)在(0,+∞)上是增函数;
(2)对m进行分类讨论,分别依据极值的定义进行分析,注意分类要做到不重不漏;
(3)要证明的问题即是当m=-1时的函数,通过构造函数分析函数的单调性得出结论.
点评:本题为导数和不等式的综合应用,涉及分类讨论的思想和极值的求解,属中档题.
f′(x)=2(x+1)+
 =
= =
= (x>0)
(x>0)当m
 时,可知f′(x)>0对任意x∈(0,+∞)恒成立,
时,可知f′(x)>0对任意x∈(0,+∞)恒成立,∴函数f(x)在(0,+∞)上是单调递增函数.
(2)由(1)知,当
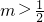 时,函数f(x)在(0,+∞)上是单调增函数,没有极值点.
时,函数f(x)在(0,+∞)上是单调增函数,没有极值点.当
 时,
时, ,函数f(x)在(0,+∞)上是单调增函数,没有极值点.
,函数f(x)在(0,+∞)上是单调增函数,没有极值点.当
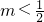 时,令f'(x)=0得,
时,令f'(x)=0得, ,
, …(6分)
…(6分)①当m≤0时,
 ,则
,则 ,
,列表:
| x | (0,x2) | x2 | (x2,+∞) |
| f'(x) | - | 0 | + |
| f(x) | ↘ | 极小值 | ↗ |
 .…(8分)
.…(8分)②当
 时,0<x1<x2<1,
时,0<x1<x2<1,列表:
| x | (0,x1) | x1 | (x1,x2) | x2 | (x2,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
 时,f(x)有极小值点
时,f(x)有极小值点 和极大值点
和极大值点 .
.综上,当m≤0时,f(x)有唯一极小值点
 ,
,当
 时,f(x)有极小值点
时,f(x)有极小值点 和极大值点
和极大值点 .…(10分)
.…(10分)(3)由(2)知,m=-1时,函数f(x)=(x-1)2-lnx,
此时,函数f(x)有唯一极小值点
 ,
,当
 时,f'(x)<0,f(x)在
时,f'(x)<0,f(x)在 上是减函数,
上是减函数,∵n≥3时,
 ,
,∴
 ,即
,即
∴n≥3时,
 .
.令函数h(x)=(x-1)-lnx(x>0),则

当x>1时,h′(x)>0,h(x)在(1,+∞)上是增函数,
∵n≥3时,1
 ,∴
,∴ f(1),即
f(1),即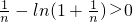
∴n≥3时,ln(n+1)-lnn

综上,当n≥3,n∈N时,不等式
 恒成立.
恒成立.分析:(1)求导数,通过m
 ,x>0,可判导数为正,可推f(x)在(0,+∞)上是增函数;
,x>0,可判导数为正,可推f(x)在(0,+∞)上是增函数;(2)对m进行分类讨论,分别依据极值的定义进行分析,注意分类要做到不重不漏;
(3)要证明的问题即是当m=-1时的函数,通过构造函数分析函数的单调性得出结论.
点评:本题为导数和不等式的综合应用,涉及分类讨论的思想和极值的求解,属中档题.

练习册系列答案
相关题目
 的最小值;
的最小值; 的最小值;
的最小值;