题目内容
已知函数f(x)=
的图象在点M(-1,f(-1))处的切线方程为x+2y+5=0.(1)求函数y=f(x)的解析式;
(2)求函数y=f(x)的单调区间.
剖析:(1)f′(1)即为x+2y+5=0的斜率,从而得出一个关于a、b的关系式.点M(-1,f(-1))在切线上,又得出一个关于a、b的等量关系式.从而可求出a、b.
(2)利用导数可求y=f(x)的单调区间.
解:(1)由函数f(x)的图象在点M(-1,f(-1))处的切线方程为x+2y+5=0,知
-1+2f(-1)+5=0,即f(-1)=-2,f′(-1)=-.
∵f′(x)=
,
∴
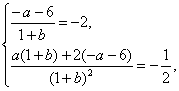
即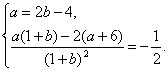
解得a=2,b=3(∵b+1≠0,b=-1舍去).
∴所求的函数解析式是f(x)=
.
(2)f′(x)=
.
令-2x2+12x+6=0,解得x1=3-2
,x2=3+2
.
当x＜3-2
或x＞3+2
时,f′(x)＜0;
当3-2
＜x＜3+2
时,f′(x)＞0.
所以f(x)=
在(-∞,3-2
)内是减函数,在(3-2
,3+2
)内是增函数,在(3+2
,+∞)内是减函数.
讲评:本题主要考查函数的单调性、导数的应用等知识,考查运用数学知识分析问题和解决问题的能力.
练习册系列答案
相关题目
已知函数f(x)=2x的反函数为f-1(x)，若f-1(a)+f-1(b)=4，则
+
的最小值为（ ）
| 1 |
| a |
| 1 |
| b |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=
的图象过点A(4，
)和B（5，1）．
①求函数f（x）的解析式；②函数f（x）的反函数；③设an=log2f（n），n是正整数，是数列的前项和Sn，解关于的不等式an≤Sn．
| ax |
| b |
| 1 |
| 2 |
①求函数f（x）的解析式；②函数f（x）的反函数；③设an=log2f（n），n是正整数，是数列的前项和Sn，解关于的不等式an≤Sn．
已知函数f(x)=
的导函数为f′（x），则f′（0）=（ ）
| xex |
| cosx |
| A、0 | ||
| B、1 | ||
C、
| ||
| D、e |
已知函数f(x)=
的图象关于直线x=
对称，则f（x）的单调递增区间为（ ）
|
| π |
| 8 |
A、[kπ-
| ||||
B、[kπ-
| ||||
C、[2kπ-
| ||||
D、[2kπ-
|