题目内容
已知数列{xn}满足x2=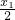 ,xn=
,xn= (xn-1+xn-2),n=3,4,….若
(xn-1+xn-2),n=3,4,….若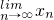 =2,则x1=
=2,则x1=
- A.

- B.3
- C.4
- D.5
B
分析:要求极限,先求通项,而条件只是一个递推关系且复杂,故宜采用归纳法猜测通项.并注意无穷递缩等比数列的极限
解答:∵ 令n=3,
令n=3,
得 ,令n=4,
,令n=4,
得 ,
,
∴ ,…,
,…, ,
,
于是xn=x1+(x2-x1)+…+(xn-xn-1)=
∴ ,x1=3.故选B
,x1=3.故选B
点评:求出前几项后,从什么角度求通项呢,一般是看差和商,采用叠加或累乘法.
分析:要求极限,先求通项,而条件只是一个递推关系且复杂,故宜采用归纳法猜测通项.并注意无穷递缩等比数列的极限
解答:∵
 令n=3,
令n=3,得
 ,令n=4,
,令n=4,得
 ,
,∴
 ,…,
,…, ,
,于是xn=x1+(x2-x1)+…+(xn-xn-1)=

∴
 ,x1=3.故选B
,x1=3.故选B点评:求出前几项后,从什么角度求通项呢,一般是看差和商,采用叠加或累乘法.

练习册系列答案
相关题目