题目内容
(本小题满分12分)
在△ABC中,BC=a,AC=b,a,b是方程x2—2 x+2=0的两个根,
x+2=0的两个根,
且2cos(A+B)=1.
求:(1)C的度数; (2)AB的长度; (3)△ABC的面积.
在△ABC中,BC=a,AC=b,a,b是方程x2—2
 x+2=0的两个根,
x+2=0的两个根,且2cos(A+B)=1.
求:(1)C的度数; (2)AB的长度; (3)△ABC的面积.
解:(1)cosC=cos[π—(A+B)]=—cos(A+ B)=—
B)=— .
.
∵0°<C<180°, ∴C=120°……………4分
(2) 由题设得 ……………………6分
……………………6分
∴AB2=AC2+BC2—2AC·BCcosC=a2+b2—2abcos120°
=a2+b2+ab= (a+b)2—ab =(2 )2—2=10.
)2—2=10.
所以AB= .……………………10分
.……………………10分
(3)S△ABC= absinC=
absinC= ×2×
×2× =
= .……………………12分
.……………………12分
 B)=—
B)=— .
.∵0°<C<180°, ∴C=120°……………4分
(2) 由题设得
 ……………………6分
……………………6分∴AB2=AC2+BC2—2AC·BCcosC=a2+b2—2abcos120°
=a2+b2+ab= (a+b)2—ab =(2
 )2—2=10.
)2—2=10.所以AB=
 .……………………10分
.……………………10分(3)S△ABC=
 absinC=
absinC= ×2×
×2× =
= .……………………12分
.……………………12分略

练习册系列答案
相关题目
 两点间的距离,今沿河
两点间的距离,今沿河 岸选取相距40米的
岸选取相距40米的 两点,测得
两点,测得 60°,
60°, =45°,
=45°, 60° ,
60° , 30°,求
30°,求


 中,角
中,角 所对的边分别为
所对的边分别为 ,向量
,向量
 ,且
,且 平行,求角
平行,求角 的大小
的大小 ,求
,求 的面积
的面积
 在舰
在舰 的正东,距离6公里,舰
的正东,距离6公里,舰 在舰
在舰 中,
中, ,
,
 ,则该四边形的面积等于( )
,则该四边形的面积等于( )








 C 4 D 4
C 4 D 4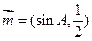 与
与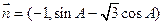 共线,其中A是△ABC的内角。
共线,其中A是△ABC的内角。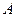 的大小; (2)若
的大小; (2)若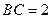 ,求
,求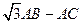 的最大值。
的最大值。 ,那么BC= ___
,那么BC= ___