题目内容
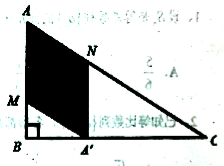
【题目】如图,某小区准备将一块闲置的直角三角形(其中![]() )土地开发成公共绿地,设计时,要求绿地部分(图中阴影部分)有公共绿地走道
)土地开发成公共绿地,设计时,要求绿地部分(图中阴影部分)有公共绿地走道![]() ,且两边是两个关于走道
,且两边是两个关于走道![]() 对称的三角形(
对称的三角形(![]() 和
和![]() ),现考虑方便和绿地最大化原则,要求
),现考虑方便和绿地最大化原则,要求![]() 点与
点与![]() 点不重合,
点不重合,![]() 点落在边
点落在边![]() 上,设
上,设![]() .
.
(1)若![]() ,绿地“最美”,求最美绿地的面积;
,绿地“最美”,求最美绿地的面积;
(2)为方便小区居民行走,设计时要求![]() 最短,求此时公共绿地走道
最短,求此时公共绿地走道![]() 的长度.
的长度.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)由![]() 中,
中,![]() ,由
,由![]() ,解得
,解得![]() ,即可求得三角形的面积;(2)因为
,即可求得三角形的面积;(2)因为![]() ,所以
,所以![]() ,则
,则![]() ,在
,在![]() 中,得到
中,得到![]() 的值,在利用三角函数的图象与性质,即可求解公共绿地走道
的值,在利用三角函数的图象与性质,即可求解公共绿地走道![]() 的长度.
的长度.
试题解析:由![]() ,得
,得![]()
设![]() ,则
,则![]() ,
,
所以在![]() 中,
中,![]()
(1)因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() 为等边三角形,
为等边三角形,
所以绿地的面积![]() .
.
(2)因为![]() ,
,
所以![]() ,则
,则![]()
又![]() ,所以在
,所以在![]() 中,
中,![]() ,故
,故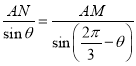 ,
,
所以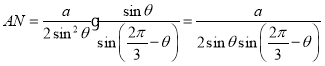
因为![]()
又![]() ,所以
,所以![]() ,
,
所以当![]() ,即
,即![]() 时,
时,![]() 最短,且
最短,且![]() ,
,
此时公共绿地走道![]()

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
