题目内容
在正方体 中,E、F分别是
中,E、F分别是 、CD的中点.(1)证明:AD⊥
、CD的中点.(1)证明:AD⊥ .(2)求AE与
.(2)求AE与 所成的角;(3)证明:面AED⊥面
所成的角;(3)证明:面AED⊥面 ;(4)设
;(4)设 ,求三棱锥
,求三棱锥 的体积
的体积 .(学完本章后做)
.(学完本章后做)
答案:略
解析:
解析:
|
证明:∵  是正方体,∴AD⊥面 是正方体,∴AD⊥面 .又 .又  面 面 .∴AD⊥ .∴AD⊥ .(2)解:取AB中点G,连结 .(2)解:取AB中点G,连结 ,FG(如图).因为F是CD的中点,所以GF、AD平行且相等.又 ,FG(如图).因为F是CD的中点,所以GF、AD平行且相等.又 、AD平行且相等,所以GF、 、AD平行且相等,所以GF、 平行且相等.故 平行且相等.故 是平行四边形, 是平行四边形, ∥ ∥ .设 .设 与AE相交于点H,则 与AE相交于点H,则 ,是AE与 ,是AE与 所成的角.因为正是 所成的角.因为正是 的中点,所以Rt△ 的中点,所以Rt△ ≌Rt△ABE, ≌Rt△ABE, ,从而 ,从而 ,即直线AE与 ,即直线AE与 所成的角为直角;(3)证明:由(1)知AD⊥ 所成的角为直角;(3)证明:由(1)知AD⊥ ,由(2)知,AE⊥ ,由(2)知,AE⊥ ,又AD∩AE=A,所以 ,又AD∩AE=A,所以 ⊥面AED.又因为D1F ⊥面AED.又因为D1F 面 面 ,所以面AED⊥面 ,所以面AED⊥面 .(4)解:连结GK, .(4)解:连结GK, .∵FG∥ .∵FG∥ ,∴FG∥面 ,∴FG∥面 .∴体积 .∴体积 .∵ .∵ ,∴面积 ,∴面积 . .
∴  . . |

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目

 中,E、F分别是中点。
中,E、F分别是中点。 ;
; ;
;
 上是否存在点P使
上是否存在点P使 ,若存在,确定点P位置;若不存在,说明理由。
,若存在,确定点P位置;若不存在,说明理由。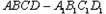 中,E、F分别是,
中,E、F分别是,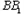 、CD的中点
、CD的中点 平面ADE.
平面ADE.

 (1)证明
(1)证明