题目内容
P是△ABC所在平面外一点；PB=PC=AB=AC，M是线段PA上一点，N是线段BC的中点，则∠MNB=
90°
90°
．分析：根据条件PB=PC=AB=AC，得到三角形ABC和PBC为等腰三角形，然后根据等腰三角形的性质，利用线面垂直的判定定理证明BC⊥平面ANP即可．
解答：解：∵N是线段BC的中点，
且PB=PC=AB=AC，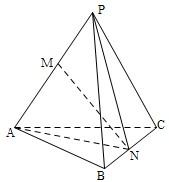
∴PN⊥BC，AN⊥BC，
又∵PN∩AN=N，
∴BC⊥平面ANP，
∵M是线段PA上一点，
∴MN?平面ANP，
∴BC⊥MN，即∠MNB=90°．
故答案为：90°．
且PB=PC=AB=AC，
∴PN⊥BC，AN⊥BC，
又∵PN∩AN=N，
∴BC⊥平面ANP，
∵M是线段PA上一点，
∴MN?平面ANP，
∴BC⊥MN，即∠MNB=90°．
故答案为：90°．
点评：本题主要考查线面垂直的判定以及线面垂直性质的应用，要求熟练掌握线面垂直的判定定理和性质定理．
练习册系列答案
名校课堂系列答案
相关题目
设P是△ABC所在平面上一点，且
-
=
-
，若△ABC的面积为2，则△PBC面积为（ ）
| CA |
| CP |
| CP |
| CB |
A、
| ||
| B、1 | ||
| C、2 | ||
| D、4 |