题目内容
设f（x）=
x3+
ax2+2bx+c的两个极值点分别是x1，x2，若x1∈（-2，-1），x2∈（-1，0），则2a+b的取值范围是（ ）
| 1 |
| 3 |
| 1 |
| 2 |
分析：求导函数，利用f（x）=
x3+
ax2+2bx+c的两个极值点分别是x1，x2，x1∈（-2，-1），x2∈（-1，0），建立不等式，利用平面区域，即可求2a+b的取值范围．
| 1 |
| 3 |
| 1 |
| 2 |
解答：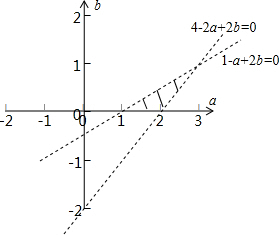
解：由题意，f′（x）=x2+ax+2b．
∵f（x）=
x3+
ax2+2bx+c的两个极值点分别是x1，x2，x1∈（-2，-1），x2∈（-1，0）
∴
，
对应的平面区域如图所示，三个顶点坐标为（1，0），（2，0），（3，1），则
在（1，0）处，2a+b2，在（3，1）处，2a+b=7，
∴2a+b的取值范围是（2，7）．
故选B．
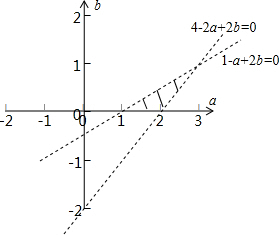解：由题意，f′（x）=x2+ax+2b．∵f（x）=
| 1 |
| 3 |
| 1 |
| 2 |
∴
|
对应的平面区域如图所示，三个顶点坐标为（1，0），（2，0），（3，1），则
在（1，0）处，2a+b2，在（3，1）处，2a+b=7，
∴2a+b的取值范围是（2，7）．
故选B．
点评：本题考查导数知识的运用，考查平面区域的运用，考查学生的计算能力，属于中档题．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目