题目内容
已知函数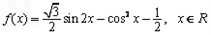
．
（1）求函数f（x）的最小值和最小正周期；
（2）设△ABC的内角A、B、C的对边分别为a，b，c，且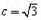
，f（C）=0，若sinB=2sinA，求a，b的值．
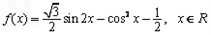．（1）求函数f（x）的最小值和最小正周期；
（2）设△ABC的内角A、B、C的对边分别为a，b，c，且
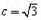，f（C）=0，若sinB=2sinA，求a，b的值．解：（1）
，
则f（x）的最小值是－2，
最小正周期是
；
（2）
，则
，
∵0＜C＜π ∴0＜2C＜2π
∴
，
∴
，
∴C=
，
∵sinB=2sinA，
由正弦定理，得
，①
由余弦定理，得c2=a2+b2-2abcos
，即a2+b2-ab=3， ②
由①②解得a=1，b=2．
，则f（x）的最小值是－2，
最小正周期是
；（2）
，则，∵0＜C＜π ∴0＜2C＜2π
∴
，∴
，∴C=
， ∵sinB=2sinA，
由正弦定理，得
，① 由余弦定理，得c2=a2+b2-2abcos
，即a2+b2-ab=3， ②由①②解得a=1，b=2．
练习册系列答案
相关题目
，如果满足；对任意
，存在常数
，都有
成立，则称
，
时，求函数
上的值域，并判断函数
上是以3为上界函数值，求实数
的取值范围；
，求函数
在
上的上界T的取值范围。
．
上的函数值的取值范围．
．
上的函数值的取值范围．