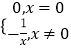题目内容

【题目】设p：不等式x2+（m﹣1）x+1＞0的解集为R；q：x∈（0，+∞），m≤x+ 恒成立．若“p且q”为假命题，“p或q”为真命题，求实数m的取值范围．

【答案】解：若p为真：判别式△＜0，则（m﹣1）2﹣4＜0，所以：﹣1＜m＜3
若q为真：：x∈（0，+∞），x+ ≥2，当且仅当x=1时取“=”所以：m≤2．（1）当p为真q为假时：2＜m＜3（2）当q为真p为假时：m≤﹣1
综上所述：m≤﹣1或2＜m＜3
【解析】根据不等式的性质分别求出命题p，q为真命题的等价条件，结合复合命题之间的关系进行求解即可．
【考点精析】解答此题的关键在于理解命题的真假判断与应用的相关知识，掌握两个命题互为逆否命题，它们有相同的真假性；两个命题为互逆命题或互否命题，它们的真假性没有关系．

练习册系列答案
相关题目

【题目】设函数f（x）=xea﹣x+bx，曲线y=f（x）在点（2，f（2））处的切线方程为y=（e﹣1）x+4，
（1）求a，b的值；
（2）求f（x）的单调区间．

【题目】椭圆： （a＞b＞0），左右焦点分别是F1 ， F2 ， 焦距为2c，若直线 与椭圆交于M点，满足∠MF1F2=2∠MF2F1 ， 则离心率是（ ）
A.
B. -1
C.
D.

【题目】已知椭圆C： (a>b>0)的一个顶点为A(2,0)，离心率为.直线y＝k(x－1)与椭圆C交于不同的两点M，N.

(1)求椭圆C的方程；

(2)当△AMN的面积为时，求k的值．

【题目】已知函数y=f（x）的定义在实数集R上的奇函数，且当x∈（﹣∞，0）时，xf′（x）＜f（﹣x）（其中f′（x）是f（x）的导函数），若a= f（ ），b=（lg3）f（lg3），c=（log2 ）f（log2 ），则（ ）
A.c＞a＞b
B.c＞b＞a
C.a＞b＞c
D.a＞c＞b

【题目】过椭圆的右焦点F作两条相互垂直的直线分别交椭圆于A，B，C，D四点，则的值为（ ）

A. B. C. 1 D.

【题目】求适合下列条件的双曲线的方程：

(1) 虚轴长为12，离心率为；

(2) 焦点在x轴上，顶点间距离为6，渐近线方程为.

【题目】已知函数f（x）的定义域为R．a，b∈R，若此函数同时满足：
①当a+b=0时，有f（a）+f（b）=0；
②当a+b＞0时，有f（a）+f（b）＞0，
则称函数f（x）为Ω函数．
在下列函数中：
①y=x+sinx；
②y=3x﹣（ ）x；
③y=
是Ω函数的为 ． （填出所有符合要求的函数序号）

【题目】已知分别是双曲线E： 的左、右焦点，P是双曲线上一点， 到左顶点的距离等于它到渐近线距离的2倍，（1）求双曲线的渐近线方程；（2）当时， 的面积为，求此双曲线的方程。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网