Question

如图，已知三棱柱ABC—A₁B₁C₁的所有棱长都相等，且侧棱垂直于底面，由B沿棱柱侧面经过棱CC₁到点A₁的最短路线长为2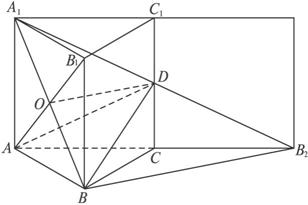,设这条最短路线与CC₁的交点为D.

（1）求三棱柱ABC—A₁B₁C₁的棱长；

（2）求四棱锥A₁—BCC₁B₁的体积；

（3）在平面A₁BD内是否存在过点D的直线与平面ABC平行？证明你的判断.

Answer 1

解:(1)如图，将侧面BB₁C₁C绕棱CC₁旋转120°使其与侧面AA₁C₁C在同一平面上，点B运动到点B₂的位置，连结A₁B₂，则A₁B₂就是由点B沿棱柱侧面经过棱CC₁到点A₁的最短路线.

设棱柱的棱长为a，则B₂C=AC=AA₁=a,

∵CD∥AA₁,∴D为CC₁的中点.

在Rt△A₁AB₂中，由勾股定理得A₁A²+AB₂²=A₁B₂²，

即a²+4a²=(2)²,解得a=2

(2)∵△ABC是正三角形,∴S_△ABC=×2²=.∴=S_△ABC·AA₁=23.

∵=,∴==.

(3)设A₁B与AB₁的交点为O,连结BB₂,OD，则OD∥BB₂,

∵BB₂平面ABC，OD平面ABC,

∴OD∥平面ABC，即在平面A₁BD内存在过点D的直线与平面ABC平行.