题目内容
定义在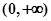 上的单调递减函数
上的单调递减函数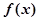 ,若
,若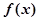 的导函数存在且满足
的导函数存在且满足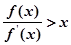 ,则下列不等式成立的是( )
,则下列不等式成立的是( )
A. | B.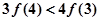 |
C.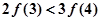 | D.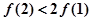 |
A
解析试题分析:∵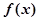 为
为 上的单调递减函数,∴
上的单调递减函数,∴ ,又∵
,又∵ ,
,
∴ >0?
>0? <0?[
<0?[ ]′<0,
]′<0,
设h(x)= ,则h(x)=
,则h(x)= 为(0,+∞)上的单调递减函数,
为(0,+∞)上的单调递减函数,
∵ >x>0,f′(x)<0,∴f(x)<0.
>x>0,f′(x)<0,∴f(x)<0.
∵h(x)= 为
为 上的单调递减函数,
上的单调递减函数,
∴ >
> ?
? >0?2f(3)﹣3f(2)>0?2f(3)>3f(2),故A正确;由2f(3)>3f(2)>3f(4),可排除C;同理可判断3f(4)>4f(3),排除B;1•f(2)>2f(1),排除D;故选A.
>0?2f(3)﹣3f(2)>0?2f(3)>3f(2),故A正确;由2f(3)>3f(2)>3f(4),可排除C;同理可判断3f(4)>4f(3),排除B;1•f(2)>2f(1),排除D;故选A.
考点:利用导数研究函数的单调性.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
已知函数 对任意的
对任意的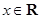 满足
满足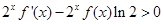 (其中
(其中 是函数
是函数 的导函数),则下列不等式成立的是( )
的导函数),则下列不等式成立的是( )
A.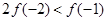 | B.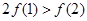 |
C.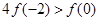 | D.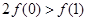 |
由直线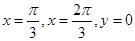 与曲线
与曲线 所围成的封闭图形的面积为( )
所围成的封闭图形的面积为( )
| A.1 | B. | C. | D.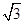 |
函数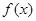 在定义域R内可导,若
在定义域R内可导,若
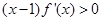 ,若
,若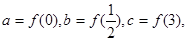 则
则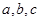 的大小关系是( )
的大小关系是( )
A.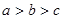 | B.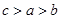 | C.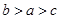 | D.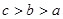 |
若函数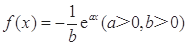 的图象在
的图象在 处的切线与圆
处的切线与圆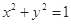 相切,则
相切,则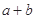 的最大值是( )
的最大值是( )
| A.4 | B.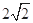 | C.2 | D.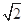 |
若函数 在R上可导,且满足
在R上可导,且满足 ,则
,则
A. | B. | C. | D. |
函数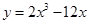 在区间
在区间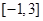 上的最大值和最小值分别为( )
上的最大值和最小值分别为( )
A.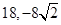 | B.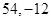 | C.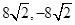 | D.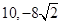 |
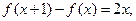 且f(0)=1.
且f(0)=1. 上,y= f(x)的图象恒在y=2x+m的图象上方,试确定实数m的范围.
上,y= f(x)的图象恒在y=2x+m的图象上方,试确定实数m的范围.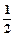 (x-1)2.若存在,求出a,b,c的值;若不存在,请说
(x-1)2.若存在,求出a,b,c的值;若不存在,请说