题目内容
椭圆 的内接矩形的最大面积的取值范围是[3b2,4b2],则该椭圆的离心率e的取值范围是
的内接矩形的最大面积的取值范围是[3b2,4b2],则该椭圆的离心率e的取值范围是
- A.
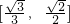
- B.

- C.

- D.

B
分析:在第一象限内取点(x,y),设x=acosθ,y=bsinθ,表示出圆的内接矩形长和宽,可得矩形的面积,由3b2≤2ab≤4b2,求得3b≤2a≤4b,平方后,可得a和c的不等式关系,即可求出离心率e的范围.
解答:在第一象限内取点(x,y),设x=acosθ,y=bsinθ,(0<θ< )
)
则椭圆的内接矩形长为2acosθ,宽为2bsinθ,
内接矩形面积为2acosθ•2bsinθ=2absin2θ≤2ab,
由已知得:3b2≤2ab≤4b2,∴3b≤2a≤4b,
平方得:9b2≤4a2≤16b2,
9(a2-c2)≤4a2≤16(a2-c2),
5a2≤9c2且12a2≥16c2,
∴ ≤
≤ ≤
≤
即e∈
故选B.
点评:本题考查了椭圆的简单性质,考查椭圆的参数方程的应用,考查学生的计算能力,属于中档题.
分析:在第一象限内取点(x,y),设x=acosθ,y=bsinθ,表示出圆的内接矩形长和宽,可得矩形的面积,由3b2≤2ab≤4b2,求得3b≤2a≤4b,平方后,可得a和c的不等式关系,即可求出离心率e的范围.
解答:在第一象限内取点(x,y),设x=acosθ,y=bsinθ,(0<θ<
 )
)则椭圆的内接矩形长为2acosθ,宽为2bsinθ,
内接矩形面积为2acosθ•2bsinθ=2absin2θ≤2ab,
由已知得:3b2≤2ab≤4b2,∴3b≤2a≤4b,
平方得:9b2≤4a2≤16b2,
9(a2-c2)≤4a2≤16(a2-c2),
5a2≤9c2且12a2≥16c2,
∴
 ≤
≤ ≤
≤
即e∈

故选B.
点评:本题考查了椭圆的简单性质,考查椭圆的参数方程的应用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
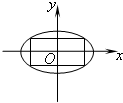 椭圆
椭圆 的内接矩形面积的最大值是________.
的内接矩形面积的最大值是________.