题目内容
11.已知平面向量$\overrightarrow{a}$=(1,m),$\overrightarrow{b}$=(2,5),$\overrightarrow{c}$=(m,3),且($\overrightarrow{a}$+$\overrightarrow{c}$)∥($\overrightarrow{a}$-$\overrightarrow{b}$),则m=( )| A. | $\frac{{-3+\sqrt{17}}}{2}$ | B. | $\frac{{3-\sqrt{17}}}{2}$ | C. | $\frac{{-3±\sqrt{17}}}{2}$ | D. | $\frac{{3±\sqrt{17}}}{2}$ |
分析 根据题意,由向量$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$的坐标计算可得($\overrightarrow{a}$+$\overrightarrow{c}$)、($\overrightarrow{a}$-$\overrightarrow{b}$)的坐标,进而由向量平行的坐标表示方法可得(m+1)×(m-5)=(m+3)×(-1),解可得m的值,即可得答案.
解答 解:根据题意,向量$\overrightarrow{a}$=(1,m),$\overrightarrow{b}$=(2,5),$\overrightarrow{c}$=(m,3),
则 $\overrightarrow a+\overrightarrow c=(m+1,m+3),\overrightarrow a-\overrightarrow b=(-1,m-5)$;
若($\overrightarrow{a}$+$\overrightarrow{c}$)∥($\overrightarrow{a}$-$\overrightarrow{b}$),
(m+1)×(m-5)=(m+3)×(-1)
解可得:$m=\frac{{3±\sqrt{17}}}{2}$;
故选:D.
点评 本题考查向量平行的坐标表示,关键是求出向量($\overrightarrow{a}$+$\overrightarrow{c}$)、($\overrightarrow{a}$-$\overrightarrow{b}$)的坐标.

练习册系列答案
相关题目
2.将函数$y=sin({2x-\frac{2π}{3}})$的图象向左平移$\frac{π}{3}$个单位所得到的图象的解析式为( )
| A. | .y=sin2x | B. | .y=-sin2x | C. | .y=cos2x | D. | y=-2cosx |
20.已知函数f(x)=log${\;}_{\frac{1}{e}}}$(x2+$\frac{1}{e}}$)-|${\frac{x}{e}}$|,则使得f(x+1)<f(2x-1)的x的范围是( )
| A. | (0,2) | B. | (-∞,0) | C. | (-∞,0)∪(2,+∞) | D. | (2,+∞) |
1.已知当x=θ时,函数f(x)=2sinx-cosx取得最大值,则sin2θ=( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | -$\frac{3}{5}$ | D. | -$\frac{4}{5}$ |
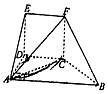 如图,几何体EF-ABCD中,DE⊥平面ABCD,CDEF是正方形,ABCD为直角梯形,AB∥CD,AD⊥DC,△ACB的腰长为$2\sqrt{2}$的等腰直角三角形.
如图,几何体EF-ABCD中,DE⊥平面ABCD,CDEF是正方形,ABCD为直角梯形,AB∥CD,AD⊥DC,△ACB的腰长为$2\sqrt{2}$的等腰直角三角形. 如图,四边形ABCD是边长为$\sqrt{2}$的正方形,CG⊥平面ABCD,DE∥BF∥CG,$DE=BF=\frac{3}{5}CG$.P为线段EF的中点,AP与平面ABCD所成角为60°.在线段CG上取一点H,使得$GH=\frac{3}{5}CG$.
如图,四边形ABCD是边长为$\sqrt{2}$的正方形,CG⊥平面ABCD,DE∥BF∥CG,$DE=BF=\frac{3}{5}CG$.P为线段EF的中点,AP与平面ABCD所成角为60°.在线段CG上取一点H,使得$GH=\frac{3}{5}CG$.