题目内容
7.已知直线a∥b,a,b与平面M斜交,a?α,b?β,且α⊥平面M,β⊥平面M,求证:α∥β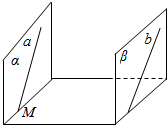
分析 要证面面平行,根据条件,要转化为线线平行,现在已有直线a∥直线b,再找一组平行直线,且分别与直线a,直线b相交,根据α⊥平面M,β⊥平面M,可找面M的垂线,由垂直于同一平面的两直线平行,问题得证.
解答 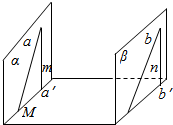 证明:令α∩M=直线a′,β∩M=直线b′.
证明:令α∩M=直线a′,β∩M=直线b′.
分别过a、b上任一点在α内、β内作a′、b′的垂线m、n.
根据两平面垂直的性质定理,
∵α⊥M,β⊥M,
∴m⊥M,n⊥M.
∴m∥n.
∵a不垂直于M,m⊥M,且a、m在α内,
∴a与m必是相交直线.又b与n在β内,且有a∥b,m∥n,
∴a∥β,m∥β.
∴α∥β.
点评 本题主要考查了面面平行的判定定理,面面垂直的性质定理,线面垂直的性质定理,综合性较强,作图是明确证明思路的关键.

练习册系列答案
相关题目
15.双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1与直线y=x+b相切,则双曲线C的离心率为( )
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{3}$ |
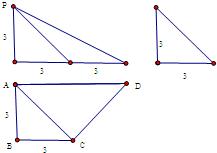 已知四棱锥P-ABCD的三视图如图所示,
已知四棱锥P-ABCD的三视图如图所示,