题目内容
20.给定平面上四点A,B,C,D,满足AB=2,AC=4,AD=6,$\overrightarrow{AB}$•$\overrightarrow{AC}$=4,则△DBC面积的最大值为$8\sqrt{3}$.分析 先利用向量的数量积公式,求出∠BAC=60°,利用余弦定理求出BC,由等面积可得A到BC的距离,即可求出△DBC面积的最大值.
解答 解:∵AB=2,AC=4,$\overrightarrow{AB}$•$\overrightarrow{AC}$=4,
∴cos∠BAC=$\frac{\overrightarrow{AB}•\overrightarrow{AC}}{|\overrightarrow{AB}||\overrightarrow{AC}|}=\frac{4}{2×4}=\frac{1}{2}$,∠BAC=60°,
∴BC=$\sqrt{{2}^{2}+{4}^{2}-2×2×4×\frac{1}{2}}=2\sqrt{3}$,
设A到BC的距离为h,则由等面积可得$\frac{1}{2}•2\sqrt{3}•h$=$\frac{1}{2}•2•4•\frac{\sqrt{3}}{2}$,
∴h=2,
∴△DBC面积的最大值为$\frac{1}{2}$•$2\sqrt{3}$(2+6)=$8\sqrt{3}$.
故答案为:$8\sqrt{3}$.
点评 本题考查向量在几何中的应用,考查三角形面积的计算,考查学生分析解决问题的能力,求出BC,A到BC的距离是解题的关键,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.已知方程x=3-lgx,下列说法正确的是( )
| A. | 方程x=3-lgx的解在区间(0,1)内 | B. | 方程x=3-lgx的解在区间(1,2)内 | ||
| C. | 方程x=3-lgx的解在区间(2,3)内 | D. | 方程x=3-lgx的解在区间(3,4)内 |
8.在△ABC中,角A,B,C所对的边a,b,c成等比数列,则角B的取值范围是( )
| A. | [$\frac{π}{3}$,π) | B. | [$\frac{π}{6}$,π) | C. | (0,$\frac{π}{3}$] | D. | (0,$\frac{π}{6}$] |
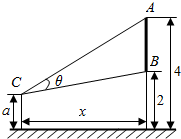 如图,墙上有一壁画,最高点A离地面4米,最低点B离地面2米.观察者从距离墙x(x>1)米,离地面高a(1≤a≤2)米的C处观赏该壁画,设观赏视角∠ACB=θ.
如图,墙上有一壁画,最高点A离地面4米,最低点B离地面2米.观察者从距离墙x(x>1)米,离地面高a(1≤a≤2)米的C处观赏该壁画,设观赏视角∠ACB=θ.