题目内容
已知下列三组条件:(1)A:α=| π |
| 6 |
| 1 |
| 2 |
分析:(1)充分性易知成立,必要性不成立.举特例sin
=
,但α≠
,
(2)将x=1代入B,B式成立,反之不成了,比如a=0时.
(3)函数y=-x2满足A,但不是减函数.
| 5π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
(2)将x=1代入B,B式成立,反之不成了,比如a=0时.
(3)函数y=-x2满足A,但不是减函数.
解答:解:(1)∵sin
=
,即由A能推出B,反之不成立,比如sin
=
,但α≠
.A是B的充分不必要条件
(2)当x=1时,x2+(a2-1)x-a2=0,反之当a=0时,方程x2-x=0的根是1,0.由B推不出A.A是B的充分不必要条件
(3)函数f(x)=-x2满足A,但在定义域R上不是减函数,A不是B的充分条件
故答案为:(1)(2)
| π |
| 6 |
| 1 |
| 2 |
| 5π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
(2)当x=1时,x2+(a2-1)x-a2=0,反之当a=0时,方程x2-x=0的根是1,0.由B推不出A.A是B的充分不必要条件
(3)函数f(x)=-x2满足A,但在定义域R上不是减函数,A不是B的充分条件
故答案为:(1)(2)
点评:此题主要考查必要条件、充分条件和充要条件的定义,是一道基础题.

练习册系列答案
相关题目
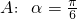 ,
,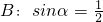 ;(2)A:x=1,B:x2+(a2-1)x-a2=0(a为实常数);(3)A:定义域为R上的函数f(x)满足f(1)>f(2),B:定义域为R的函数f(x)是单调减函数.其中A是B的充分不必要条件的是________.(填写所有满足要求的条件组的序号)
;(2)A:x=1,B:x2+(a2-1)x-a2=0(a为实常数);(3)A:定义域为R上的函数f(x)满足f(1)>f(2),B:定义域为R的函数f(x)是单调减函数.其中A是B的充分不必要条件的是________.(填写所有满足要求的条件组的序号)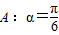 ,
,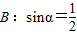 ;(2)A:x=1,B:x2+(a2-1)x-a2=0(a为实常数);(3)A:定义域为R上的函数f(x)满足f(1)>f(2),B:定义域为R的函数f(x)是单调减函数.其中A是B的充分不必要条件的是 .(填写所有满足要求的条件组的序号)
;(2)A:x=1,B:x2+(a2-1)x-a2=0(a为实常数);(3)A:定义域为R上的函数f(x)满足f(1)>f(2),B:定义域为R的函数f(x)是单调减函数.其中A是B的充分不必要条件的是 .(填写所有满足要求的条件组的序号)