题目内容
已知数列![]() 中,
中,![]() ,且
,且
![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求证:对一切![]() ,有
,有![]() .
.
解 (1)由已知,对![]() 有
有 ![]() ,
,
两边同除以n,得 ![]() ,
,
即 ![]() , ……………………5分
, ……………………5分
于是,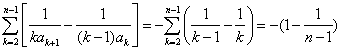 ,
,
即 ![]() ,
,
所以 ![]() ,
,![]() .
.
又![]() 时也成立,故
时也成立,故![]() . ……………………10分
. ……………………10分
(2)当![]() ,有
,有
![]() ,………………15分
,………………15分
所以![]() 时,有
时,有
![]()
![]()
又![]() 时,
时,![]()
故对一切![]() ,有
,有![]() . ……………………20分
. ……………………20分

练习册系列答案
相关题目
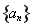



 中, a2=7,且an =an+1-6(n∈
中, a2=7,且an =an+1-6(n∈ ),则前n项和Sn=" (" )
),则前n项和Sn=" (" ) B. n2 C.
B. n2 C. D.3n2
–2n
D.3n2
–2n 中,
中,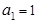 ,且
,且 ,则
,则 =( )
=( )