题目内容
已知数列![]() 中,
中,![]() ,且
,且![]()
![]()
(Ⅰ) 求数列![]() 的通项公式;
的通项公式;
(Ⅱ) 令![]()
![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,试比较
,试比较![]() 与
与![]() 的大小;
的大小;
(Ⅲ) 令![]()
![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() .求证:对任意
.求证:对任意![]() ,
,
都有 ![]() 。
。
(Ⅰ) ![]()
(Ⅱ) ![]()
(Ⅲ)证明见解析。
解析:
(Ⅰ)由题![]() 知,
知, ![]() ,
,
由累加法,当![]() 时,
时,![]()
代入![]() ,得
,得![]() 时,
时,![]()
又![]() ,故
,故![]() . ................4分
. ................4分
(II)![]() 时,
时,![]() .
.
方法1:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
猜想当![]() 时,
时,![]() . ................6分
. ................6分
下面用数学归纳法证明:
①当![]() 时,由上可知
时,由上可知![]() 成立;
成立;
②假设![]() 时,上式成立,即
时,上式成立,即![]() .
.
当![]() 时,左边
时,左边![]()
![]() ,所以当
,所以当![]() 时成立.
时成立.
由①②可知当![]() 时,
时,![]() .
. ![]()
综上所述:当![]() 时,
时,![]() ;当
;当![]() 时,
时, ![]() ;
;
当![]() 时,
时,![]() .
. ![]() ...............10分
...............10分
方法2:![]()
记函数![]()
所以![]() .........6分
.........6分
则![]()
所以![]() .
.
由于![]() ,此时
,此时![]() ;
;
![]() ,此时
,此时![]() ;
;
![]() ,此时
,此时![]() ;
;
由于,![]() ,故
,故![]() 时,
时,![]() ,此时
,此时![]() .
.
综上所述:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() . ...........10分
. ...........10分
(III)![]()
当![]() 时,
时,![]()
所以当![]() 时
时![]()
+![]() .
.
且![]()
故对![]() ,
,![]() 得证. .................14
得证. .................14

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
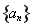



 中, a2=7,且an =an+1-6(n∈
中, a2=7,且an =an+1-6(n∈ ),则前n项和Sn=" (" )
),则前n项和Sn=" (" ) B. n2 C.
B. n2 C. D.3n2
–2n
D.3n2
–2n 中,
中, ,且
,且 ,则
,则 =( )
=( )