题目内容
△ABC的三个内角A,B,C所对的边分别为a,b,c,向量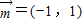 ,
,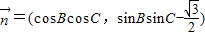 ,且
,且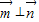 .
.(1)求A的大小;
(2)现在给出下列三个条件:①a=1;②
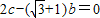 ;③B=45°,试从中选择两个条件以确定△ABC,求出所确定的△ABC的面积.
;③B=45°,试从中选择两个条件以确定△ABC,求出所确定的△ABC的面积.
【答案】分析:(1)利用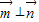 ,推出cos(B+C)=
,推出cos(B+C)=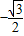 ,然后求出A=30°.
,然后求出A=30°.
(2)方案一:选择①②,可以确定△ABC,通过余弦定理,得c=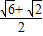 ,求出S△ABC.
,求出S△ABC.
方案二:选择①③,可以确定△ABC,由正弦定理的c,然后求出S△ABC.
解答:解:(1)因为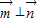 ,所以-cosBcosC+sinBsinC-
,所以-cosBcosC+sinBsinC-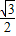 =0,
=0,
所以cos(B+C)=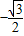 ,
,
因为A+B+C=π,所以cos(B+C)=-cosA,
所以cosA=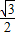 ,A=30°.
,A=30°.
(2)方案一:选择①②,可以确定△ABC,
因为A=30°,a=1,2c-(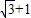 )b=0,
)b=0,
由余弦定理,得:12=b2+(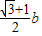 )2-2b•
)2-2b•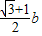 •
•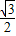 ,
,
整理得:b2=2,b=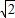 ,c=
,c=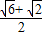 ,
,
所以S△ABC=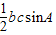 =
=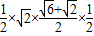 =
=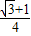 .
.
方案二:选择①③,可以确定△ABC,
因为A=30°,a=1,B=45°,C=105°,
又sin105°=sin(45°+60°)=sin45°cos60°+sin60°cos45°=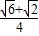 .
.
由正弦定理的c=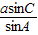 =
=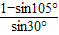 =
=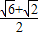 ,
,
所以S△ABC=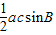 =
=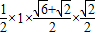 =
=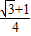 .
.
点评:本题考查向量的垂直,正弦定理的应用,考查分析问题解决问题的能力.
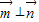 ,推出cos(B+C)=
,推出cos(B+C)=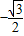 ,然后求出A=30°.
,然后求出A=30°.(2)方案一:选择①②,可以确定△ABC,通过余弦定理,得c=
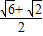 ,求出S△ABC.
,求出S△ABC.方案二:选择①③,可以确定△ABC,由正弦定理的c,然后求出S△ABC.
解答:解:(1)因为
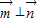 ,所以-cosBcosC+sinBsinC-
,所以-cosBcosC+sinBsinC-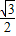 =0,
=0,所以cos(B+C)=
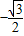 ,
,因为A+B+C=π,所以cos(B+C)=-cosA,
所以cosA=
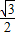 ,A=30°.
,A=30°.(2)方案一:选择①②,可以确定△ABC,
因为A=30°,a=1,2c-(
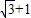 )b=0,
)b=0,由余弦定理,得:12=b2+(
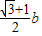 )2-2b•
)2-2b•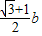 •
•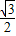 ,
,整理得:b2=2,b=
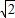 ,c=
,c=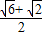 ,
,所以S△ABC=
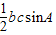 =
=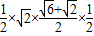 =
=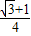 .
.方案二:选择①③,可以确定△ABC,
因为A=30°,a=1,B=45°,C=105°,
又sin105°=sin(45°+60°)=sin45°cos60°+sin60°cos45°=
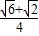 .
.由正弦定理的c=
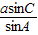 =
=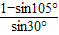 =
=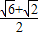 ,
,所以S△ABC=
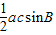 =
=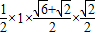 =
=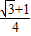 .
.点评:本题考查向量的垂直,正弦定理的应用,考查分析问题解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知a,b,c分别是△ABC的三个内角A,B,C所对的边,若a=1,b=
,A+C=2B,则sinC=( )
| 3 |
| A、0 | B、2 | C、1 | D、-1 |