题目内容
11.已知曲线$\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{{k}^{2}-k}$=1,当曲线表示圆时k的取值是-1或2,当曲线表示焦点在y轴上的椭圆时k的取值范围是k<-1或k>2,当曲线表示双曲线时k的取值范围是0<k<1.分析 利用曲线表示圆、焦点在y轴上的椭圆、双曲线建立k的不等式,即可求得k的取值范围.
解答 解:当曲线表示圆时,2=k2-k,∴k=-1或2;
当曲线表示焦点在y轴上的椭圆时,k2-k>2,∴k<-1或k>2;
当曲线表示双曲线时,k2-k<0,∴0<k<1.
故答案为:-1或2;k<-1或k>2;0<k<1.
点评 本题考查曲线表示圆、焦点在y轴上的椭圆、双曲线的条件,考查学生的计算能力,比较基础.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
6.在平行四边形ABCD中,AC与BD交于点O,E是OB的中点,若$\overrightarrow{AC}$=$\overrightarrow a$,$\overrightarrow{BD}$=$\overrightarrow b$,则$\overrightarrow{CE}$等于( )
| A. | -$\frac{1}{2}\overrightarrow{a}+\frac{1}{4}\overrightarrow{b}$ | B. | $\frac{1}{2}\overrightarrow{a}-\frac{1}{4}\overrightarrow{b}$ | C. | $\frac{1}{2}\overrightarrow{a}+\frac{1}{4}\overrightarrow{b}$ | D. | -$\frac{1}{2}\overrightarrow{a}-\frac{1}{4}\overrightarrow{b}$ |
16.根据下面某工程的工作明细表:
(1)画出工作流程图;
(2)指出关键路径;
(3)确定完成工程的最短总工期.
| 工作代码 | 紧前工作 | 工期(天) |
| A | 无 | 7 |
| B | 无 | 3 |
| C | 无 | 1 |
| D | C | 3 |
| E | A,B,D | 3 |
| F | E | 2 |
| G | A,B,D | 2 |
| H | F,G | 1 |
(2)指出关键路径;
(3)确定完成工程的最短总工期.
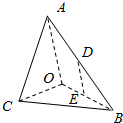 如图,在三棱锥A-BOC中,AO⊥平面COB,∠OAB=∠OAC=$\frac{π}{6}$,AB=AC=2,BC=$\sqrt{2}$,D,E分别为AB,OB的中点.
如图,在三棱锥A-BOC中,AO⊥平面COB,∠OAB=∠OAC=$\frac{π}{6}$,AB=AC=2,BC=$\sqrt{2}$,D,E分别为AB,OB的中点. 如图,在Rt△ABC中,∠B=30°,∠C=60°,AC=a,动点P,Q自A出发分别沿边界按ABCA的方向及ACBA的方向运动,它们的速度之比是1:3,当P,Q相遇时,停止运动,点P所走过的路程为x,△APQ的面积为y,写出y关于x的函数关系式,并求出定义域.
如图,在Rt△ABC中,∠B=30°,∠C=60°,AC=a,动点P,Q自A出发分别沿边界按ABCA的方向及ACBA的方向运动,它们的速度之比是1:3,当P,Q相遇时,停止运动,点P所走过的路程为x,△APQ的面积为y,写出y关于x的函数关系式,并求出定义域.