Question

如图，在棱长为1的正方体ABCD-A₁B₁C₁D₁中，P是AC与BD的交点，M是CC₁的中点．
（1）求证：A₁P⊥平面MBD；
（2）求直线B₁M与平面MBD所成角的正弦值；
（3）求平面ABM与平面MBD所成锐角的余弦值．

Answer 1

分析：（1）以D为坐标原点，向量

DA

，

DC

，

DD1

为单位正交基向量，建立空间直角坐标系D-xyz．分别求出向量

A1P

，

DB

，

DM

的坐标，根据

A1P

•

DB

=0，

A1P

•

DM

=0，得到A₁P⊥DB，A₁P⊥DM，由线面垂直的判定定理得A₁P⊥平面MBD；
（2）分别求出直线B₁M的方向向量与平面MBD的法向量，代入向量夹角公式，即可得到直线B₁M与平面MBD所成角的正弦值；
（3）分别求出平面ABM与平面MBD的法向量，代入向量夹角公式，即可得到平面ABM与平面MBD所成锐角的余弦值．

解答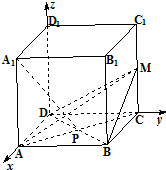：解：（1）证明：如图，以D为坐标原点，向量

DA

，

DC

，

DD1

为单位正交基向量，
建立空间直角坐标系D-xyz．则P（

1

2

，

1

2

，0），M（0，1，

1

2

）．

A1P

=（-

1

2

，

1

2

，-1），

DB

=（1，1，0），

DM

=（0，1，

1

2

），所以

A1p•

DB

=0，

A1p•

DM

=0．
所以

A1p

⊥

DB

，

A1p

⊥

DM

又因为BD∩DM=D，所以A₁P⊥平面MBD；
（2）由（1）可知，可取

n

=（1，-1，2）为平面MBD的一个法向量．
又

.

B1M

=（-1，0，-

1

2

），
所以cos＜

n

，

AM

＞=-

2 5

5

所以直线AM与平面MBD所成角的正弦值为

2 5

5

．
（3）

AB

=（0，1，0），

BM

=（-1，0，

1

2

）．
设

n

₁=（x，y，z）为平面ABM的一个法向量，则

n1• AB =0 n1• BM =0

解得

y=0 -x+ 1 2 z=0

即

y=0 z=2x

，故可取

n

₁=（1，0，2）．
由（1）可知，可取

n

=（1，-1，2）为平面MBD的一个法向量．
所以cos＜

n

，

n

₁＞=

1+4

5 × 6

=

30

6

．
所以平面ABM与平面MBD所成锐角的余弦值为

30

6

．

点评：本题考查的知识点是二面角的平面角及求法，直线与平面垂直的判定，直线与平面所成的角，其中建立适当的坐标系，将空间直线与平面的垂直、平行问题，线面夹角问题，二面角问题转化为向量夹角问题是解答本题的关键．