题目内容

在平行六面体ABCD—A1B1C1D1中，已知AB=5，AD=4，AA1=3，AB⊥AD，∠A1AB=∠A1AD=.

（1）求证：顶点A1在底面ABCD的射影在∠BAD的角平分线上；?

（2）若M、N分别在D1C1、B1C1上且D1M=2，B1N=2，求BN与CM所成的角.

提示：过A1作A1O⊥面ABCD于O，设∠BAO=θ1,∠DAO=θ2,∠A1AO=α.?

（1）证明：依题意，cos∠A1AB=cos∠A1AO·cos∠BAO,?

即cos=cosα·cosθ1.?

同理,cos=cosα·cosθ2.?

∴cosθ1=cosθ2.又θ1与θ2均为锐角，?

∴θ1=θ2,即AO是∠BAD的平分线.?

∴A1在底面ABCD的射影在∠BAD的平分线上.?

（2）解析：∵?

=,?

，?

且AB⊥AD,?

∴?

=?

=32-·3·5·cos+·4·3·cos-×1×5×cos?

=.?

又||=|+|?

=?

=，?

||=||?

=?

=3.?

cos〈,〉=.?

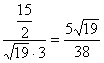∴BN与CM所成角为arccos.

练习册系列答案
相关题目
如图，在平行六面体ABCD-A1B1C1D1中，O为AC与BD的交点，若
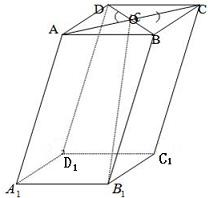
A1B1
=
a
，
A1D1
=
b
，
AA1
=
c
，则向量
B1O
等于（　　）
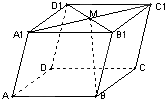精英家教网
A、
1
2
a
+
1
2
b
+
c
B、
1
2
a
-
1
2
b
+
c
C、-
1
2
a
+
1
2
b
+
c
D、-
1
2
a
-
1
2
b
+
c
精英家教网如图：在平行六面体ABCD-A1B1C1D1中，M为A1C1与B1D1的交点．若
AB
=
a
，
AD
=
b
，
AA1
=
c
，则下列向量中与
BM
相等的向量是（　　）
A、-
1
2
a
+
1
2
b
+
c
B、
1
2
a
+
1
2
b
+
c
C、-
1
2
a
-
1
2
b
+
c
D、
1
2
a-
1
2
b+c
在平行六面体ABCD-A1B1C1D1中，向量
D1A
、
D1C
、
A1C1
是（　　）
已知在平行六面体ABCD-A1B1C1D1中，AB=AD=AA1=1，且∠BAD=∠BAA1=∠DAA1=60°，求AC1的长．
在平行六面体ABCD-A1B1C1D1中，
AC
=
a
，
BD
=
b
，
AC1
=
c
，试用
a
、
b
、
c
表示
BD1
=
b
+
c
-
a
b
+
c
-
a
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网