题目内容
【题目】已知抛物线![]() ,过
,过![]() 的直线
的直线![]() 与抛物线C交于
与抛物线C交于![]() 两点,点A在第一象限,抛物线C在
两点,点A在第一象限,抛物线C在![]() 两点处的切线相互垂直.
两点处的切线相互垂直.
(1)求抛物线C的标准方程;
(2)若点P为抛物线C上异于![]() 的点,直线
的点,直线![]() 均不与
均不与![]() 轴平行,且直线AP和BP交抛物线C的准线分别于
轴平行,且直线AP和BP交抛物线C的准线分别于![]() 两点,
两点,![]() .
.
(i)求直线![]() 的斜率;
的斜率;
(ⅱ)求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)(i)
;(2)(i)![]() ;(ⅱ)4.
;(ⅱ)4.
【解析】
(1)利用导数的几何意义分别求得![]() 处切线的斜率,再根据斜率相乘为
处切线的斜率,再根据斜率相乘为![]() ,可得
,可得![]() 的值,即可得答案;
的值,即可得答案;
(2)(i)根据![]() 可得点
可得点![]() 横坐标的关系,再结合韦达定理,可求得斜率;
横坐标的关系,再结合韦达定理,可求得斜率;
(ii)由(i)易知![]() ,设
,设![]() ,则
,则![]() ,再分别求出点
,再分别求出点![]() 的横坐标用
的横坐标用![]() 表示,利用换元法可求得
表示,利用换元法可求得![]() 的最值.
的最值.
(1)设![]() .
.
抛物线C的方程可化为![]() .
.
抛物线C在![]() 两点处的切线的斜率分别为
两点处的切线的斜率分别为![]() .
.
由题可知直线l的斜率存在,故可设直线1的方程为![]() ,
,
联立![]() ,消去y可得
,消去y可得![]() ,
,
![]() .
.
![]() ,解得
,解得![]() .
.
∴抛物线C的标准方程为![]() ;
;
(2)(i)由(1)可得![]()
由![]() ,可得
,可得![]() ,
,
又点A在第一象限,解得![]() .
.
∴直线AB的斜率为![]() ;
;
(ii)由(i)易知![]() .
.
设![]() ,则
,则![]() .
.
由题可知![]() ,故
,故![]() 且
且![]() .
.
∴直线AP的斜率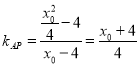 ,同理可得
,同理可得![]() .
.
∴直线![]() ,当
,当![]() 时,
时,![]() .
.
直线![]() ,当
,当![]() 时,
时,![]() .
.
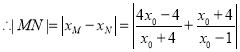 .
.
令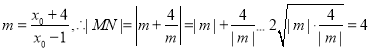 ,
,
当且仅当![]() ,即
,即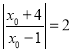 ,也即
,也即![]() 或
或![]() 时,
时,![]() 取得最小值4.
取得最小值4.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案【题目】为了解某地网民浏览购物网站的情况,从该地随机抽取100名网民进行调查,其中男性、女性人数分别为45和55.下面是根据调查结果绘制的网民日均浏览购物网站时间的频率分布直方图,将日均浏览购物网站时间不低于40分钟的网民称为“网购达人”,已知“网购达人”中女性有10人.

(1)根据已知条件完成下面的![]() 列联表,并判断是否有90%的把握认为是否为“网购达人”与性别有关;
列联表,并判断是否有90%的把握认为是否为“网购达人”与性别有关;
非网购达人 | 网购达人 | 总计 | |
男 | |||
女 | 10 | ||
总计 |
(2)将上述调査所得到的频率视为概率,现在从该地的网民中随机抽取3名,记被抽取的3名网民中的“网购达人”的人数为X,求X的分布列、数学期望![]() 和方差
和方差![]() .
.
参考公式: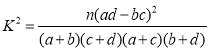 ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |