题目内容
【题目】已知函数![]()
(1)若存在正数![]() ,使
,使![]() 恒成立,求实数
恒成立,求实数![]() 的最大值;
的最大值;
(2)设![]() ,若
,若![]() 没有零点,求实数
没有零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)1(2) ![]()
【解析】
(1)先对函数求导,再由导数研究出原函数的单调性,确定最大值,结合条件中的不等式,分离参数![]() ,得到
,得到![]() 关于
关于![]() 的函数就,再利用导数求出
的函数就,再利用导数求出![]() 的最大值;
的最大值;
(2)把![]() 的值代入
的值代入![]() ,利用导数研究
,利用导数研究![]() 的单调区间,要使
的单调区间,要使![]() 没有零点,则
没有零点,则![]() 的最小值大于0,然后分类参数
的最小值大于0,然后分类参数![]() ,即可求出实数
,即可求出实数![]() 的取值范围。
的取值范围。
解:(1) ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上是增函数;
上是增函数;
当![]() 时,
时,![]() 在
在![]() 上是减函数,
上是减函数,
故当![]() 时,函数
时,函数![]() 取得极大值
取得极大值![]() .
.
若对任意![]() 恒成立,
恒成立,
当且仅当![]() ,即
,即![]() 成立.
成立.
设![]() ,则
,则![]() .
.
当![]() 时,
时,![]() 是增函数;
是增函数;
当![]() 时,
时,![]() 是减函数,
是减函数,
所以当![]() 时,
时,![]() 取得极大值
取得极大值![]() ,即
,即![]() .
.
所以![]() ,即实数
,即实数![]() 的最大值是
的最大值是![]() .
.
(2)![]() ,所以
,所以
![]() ,
,
设![]() ,则
,则![]() 在
在![]() 上是增函数,
上是增函数,
又![]() ,
,
所以![]() 在区间
在区间![]() 内存在唯一零点
内存在唯一零点![]() ,即
,即![]() .
.
当![]() 时,
时,![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() ,所以
,所以![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,所以
上是增函数,所以![]() .
.
因为![]() 没有零点,所以
没有零点,所以![]() ,
,
即![]() ,
,
所以![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目
【题目】现有一环保型企业,为了节约成本拟进行生产改造,现将某种产品产量![]() 与单位成本
与单位成本![]() 统计数据如下:
统计数据如下:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
产量(千件) | 2 | 3 | 4 | 5 | 4 | 5 |
单位成本(元/件) | 73 | 72 | 71 | 73 | 69 | 68 |
(Ⅰ)试确定回归方程![]() ;
;
(Ⅱ)指出产量每增加1000件时,单位成本平均下降多少?
(Ⅲ)假定单位成本为70元/件时,产量应为多少件?
(参考公式: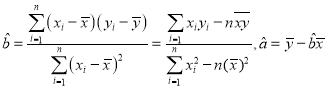 .)
.)
(参考数据![]()
![]() )
)