题目内容
(满分12分)
(1)已知△ABC三个顶点的坐标分别为A(4,1),B(0,3),C(2,4),边AC的中点为D,求AC边上中线BD所在的直线方程并化为一般式;
(2)已知圆C的圆心是直线 和
和 的交点上且与直线
的交点上且与直线 相切,求圆C的方程.
相切,求圆C的方程.
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)先根据中点坐标公式得出 的中点的坐标,再根据直线方程的两点式写出
的中点的坐标,再根据直线方程的两点式写出 的方程,再化成一般式即可;(2)联立两直线的方程,求出交点坐标即圆心坐标,再利用点到直线的距离公式求出圆的半径,写出圆的方程即可.
的方程,再化成一般式即可;(2)联立两直线的方程,求出交点坐标即圆心坐标,再利用点到直线的距离公式求出圆的半径,写出圆的方程即可.
解题思路: 1.直线的方程有五种形式(点斜式、斜截式、两点式、截距式、一般式),要注意各种形式的适用条件,合理选用;2.圆的方程要注意圆心定位置,半径定大小.
试题解析:(1)∵A(4,1),C(2,4),
∴AC边的中点D的坐标为 ,
,
又B(0,3),(2分)
由直线两点式,得中线BD所在的直线方程为 (6分)
(6分)
即 (6分)
(6分)
(2)解方程组 得
得 (9分)
(9分)
由点 到直线
到直线 距离得
距离得
∴圆的半径为4 (11分)
∴圆C的方程为: (12分)
(12分)
考点:1.直线的方程;2.圆的方程;3.直线与圆的位置关系.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
 的值域为 .
的值域为 . 是公差不为零的等差数列,并且
是公差不为零的等差数列,并且 是等比数列
是等比数列 的相邻三项,若
的相邻三项,若 ,则
,则 等于( )
等于( ) B.
B. C.
C. D.
D.
 中,
中, 分别为
分别为 中点,则异面直线
中点,则异面直线 与
与 所成角的余弦值为
所成角的余弦值为
 B.
B. C.
C. D.
D.
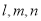 是三条不同的直线,
是三条不同的直线,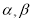 是两个不同的平面,下列命题为真命题的是 ( )
是两个不同的平面,下列命题为真命题的是 ( )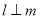 ,
,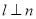 ,
,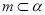 ,
,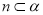 ,则
,则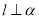 ,
,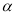 ∥
∥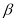 ,
, ,则
,则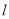 ∥
∥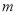 ,
,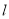 ∥
∥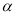
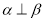 ,
,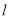 ∥
∥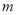
 B、6 C、4 D、
B、6 C、4 D、
 是抛物线
是抛物线 上的动点,点
上的动点,点 在
在 轴上的射影是
轴上的射影是 ,
, ,则
,则 的最小值是 .
的最小值是 .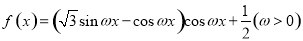 的周期为
的周期为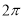 .
.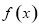 的解析式;
的解析式;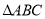 中,角A、B、C的对边分别是
中,角A、B、C的对边分别是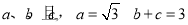 ,
,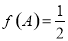 ,求
,求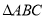 的面积.
的面积.