题目内容
正方形ABCD的两顶点A、B在抛物线y=x2上,两顶点C、D在直线y=x-4上,求正方形的边长.分析:根据正方形的性质设出AB的方程代入抛物线方程,利用韦达定理求得x1+x2和x1x2的表达式,进而利用弦长公式求得AB的长,利用平行线之间的距离公式求得AB到直线CD的距离,利用变长相等求得b,最后把b代入两直线的距离公式中即可.
解答:解:设AB方程 y=x+b,
代入抛物线方程得x2-x-b=0
∴x1+x2=1,x1x2=-b
∴|AB|=
=
•
直线AB与y=x-4距离为
∵ABCD是正方形.
∴
•
=
解得:b=2或6,
∴正方形边长=3
或者5
.
代入抛物线方程得x2-x-b=0
∴x1+x2=1,x1x2=-b
∴|AB|=
| 2 |
| (x1+x2) 2-4x1x2 |
| 2 |
| 1+4b |
直线AB与y=x-4距离为
| |4+b| | ||
|
∵ABCD是正方形.
∴
| 2 |
| 1+4b |
| |4+b| | ||
|
解得:b=2或6,
∴正方形边长=3
| 2 |
| 2 |
点评:本题主要考查了直线与圆锥曲线的问题.考查了学生分析问题和解决问题的能力.

练习册系列答案
相关题目
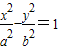 (a>0,b>0)的两个焦点,若F1,F2,P(0,2b)是正三角形的三个顶点,则双曲线的离心率为 ;经过抛物线y=
(a>0,b>0)的两个焦点,若F1,F2,P(0,2b)是正三角形的三个顶点,则双曲线的离心率为 ;经过抛物线y=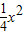 的焦点作直线交抛物线于A(x1,y1),B(x2,y2)两点,若y1+y2=5,则线段AB的长等于 .
的焦点作直线交抛物线于A(x1,y1),B(x2,y2)两点,若y1+y2=5,则线段AB的长等于 .