题目内容
在平面上有两个区域M和N,其中M满足
,N由t≤x≤t+1确定,当t=0时,M和N公共部分的面积是
;当0≤t≤1时,M和N的公共部分面积的最大值为
.
|
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
分析:先画出可行域M,再画出可行域N,由于区域N为动区域,故讨论t的范围,以确定两区域的公共部分,最后建立面积关于t的二次函数,利用配方法求最值即可
解答:解:画出区域M如图:
由
得A(1,1)
当t=0时,N为0≤x≤1,M和N公共部分的面积是
S△AOB=
当t=1时,N为1≤x≤2,M和N公共部分的面积是
S△AOB=
当0<t<1时,0<t≤x≤t+1<2,M和N公共部分的面积S=S△AOB-
×t×t-
×(1-t)×(1-t)=1-
-
=-t2+t+
∴当t=
时,面积最大为-
+
+
=
故答案为

由
|
当t=0时,N为0≤x≤1,M和N公共部分的面积是
| 1 |
| 2 |
| 1 |
| 2 |
当t=1时,N为1≤x≤2,M和N公共部分的面积是
| 1 |
| 2 |
| 1 |
| 2 |
当0<t<1时,0<t≤x≤t+1<2,M和N公共部分的面积S=S△AOB-
| 1 |
| 2 |
| 1 |
| 2 |
| t2 |
| 2 |
| 1-2t+t2 |
| 2 |
| 1 |
| 2 |
∴当t=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
故答案为
| 1 |
| 2 |
| 3 |
| 4 |
点评:本题主要考查了线性规划的思想,建立函数模型解决问题的方法,数形结合的思想方法,配方法求二次函数的值域,属基础题

练习册系列答案
相关题目
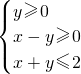 ,N由t≤x≤t+1确定,当t=0时,M和N公共部分的面积是________;当0≤t≤1时,M和N的公共部分面积的最大值为________.
,N由t≤x≤t+1确定,当t=0时,M和N公共部分的面积是________;当0≤t≤1时,M和N的公共部分面积的最大值为________. ,N由t≤x≤t+1确定,当t=0时,M和N公共部分的面积是 ;当0≤t≤1时,M和N的公共部分面积的最大值为 .
,N由t≤x≤t+1确定,当t=0时,M和N公共部分的面积是 ;当0≤t≤1时,M和N的公共部分面积的最大值为 .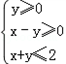 ,N由t≤x≤t+1确定,
,N由t≤x≤t+1确定,