题目内容
已知过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 、
、![]() 两点,
两点,![]() 、
、![]() 分别是该抛物线在
分别是该抛物线在![]() 、
、![]() 两点处的切线,
两点处的切线,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 与直线
与直线![]() 的交点.
的交点.
(1)求直线![]() 的斜率的取值范围;
的斜率的取值范围;
(2)试比较![]() 与
与![]() 的大小,并说明理由.
的大小,并说明理由.
(1)直线![]() 的斜率的取值范围:k<﹣1 或 k >1;(2)
的斜率的取值范围:k<﹣1 或 k >1;(2)![]() .
.
解析:
1)设直线![]() ,则
,则
![]() ,
,
依题意,有![]() 或
或![]() ;
;
(2)由![]() ,所以抛物线在
,所以抛物线在![]() 处的切线
处的切线![]() 的方程为
的方程为
![]() ,即
,即![]() .
.
令![]() ,得
,得![]() .
.
同理,得![]() .
.
注意到![]() 、
、![]() 是方程①的两个实根,故
是方程①的两个实根,故![]() ,即
,即![]() ,从而有
,从而有
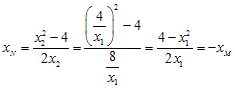 ,
,
因此,![]() .
.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
22.(本题满分15分)已知抛物线C的顶点在原点,焦点在y轴正半轴上,点 到其准线的距离等于5.
到其准线的距离等于5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)如图,过抛物线C的焦点的直线从左到右依次与抛物线C及圆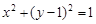 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明 为定值;
为定值;
|
 且
且 交于点M,求
交于点M,求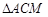 与
与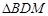 面积之和的最小值.
面积之和的最小值.
(本小题满分15分)
已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5。
(I)求抛物线G的方程;
(II)如图,过抛物线G的焦点的直线依次与抛物线G及圆![]() 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明![]() 为定值;
为定值;
|
 已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5.
已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5.
 到其准线的距离等于5.
到其准线的距离等于5. 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明 为定值;
为定值; 且
且 与
与 面积之和的最小值.
面积之和的最小值.
 |BD|为定值;
|BD|为定值;
