题目内容
由正方体ABCD-A1B1C1D1的8个顶点构成的所有三角形中,任取其中的两个不共面的概率为
- A.

- B.

- C.

- D.

A
分析:先计算能构成多少个三角形,再将共面的情况剔除,即通过对立事件就可以计算不共面的概率.
解答:正方体有8个顶点,∴任意取构成的三角形个数为C83=56,
即从56个三角形中任取两个三角形,
现共面的情况为表面6个面与6个对角面,每个面构成4个三角形,
设任取两个三角形不共面为事件“A”,
∴P(A)=1- =1-
=1- =
= ,
,
故选A.
点评:本题考查等可能事件的概率,如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)= ,本题要结合对立事件的概率解决较好,属于中档题.
,本题要结合对立事件的概率解决较好,属于中档题.
分析:先计算能构成多少个三角形,再将共面的情况剔除,即通过对立事件就可以计算不共面的概率.
解答:正方体有8个顶点,∴任意取构成的三角形个数为C83=56,
即从56个三角形中任取两个三角形,
现共面的情况为表面6个面与6个对角面,每个面构成4个三角形,
设任取两个三角形不共面为事件“A”,
∴P(A)=1-
 =1-
=1- =
= ,
,故选A.
点评:本题考查等可能事件的概率,如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
 ,本题要结合对立事件的概率解决较好,属于中档题.
,本题要结合对立事件的概率解决较好,属于中档题. 
练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
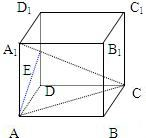 由正方体ABCD-A1B1C1D1的顶点A作这正方体的对角线A1C的垂线,垂足为E,证明A1E:EC=1:2.
由正方体ABCD-A1B1C1D1的顶点A作这正方体的对角线A1C的垂线,垂足为E,证明A1E:EC=1:2. 由正方体ABCD-A1B1C1D1的顶点A作这正方体的对角线A1C的垂线,垂足为E,证明A1E:EC=1:2.
由正方体ABCD-A1B1C1D1的顶点A作这正方体的对角线A1C的垂线,垂足为E,证明A1E:EC=1:2.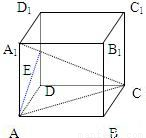 由正方体ABCD-A1B1C1D1的顶点A作这正方体的对角线A1C的垂线,垂足为E,证明A1E:EC=1:2.
由正方体ABCD-A1B1C1D1的顶点A作这正方体的对角线A1C的垂线,垂足为E,证明A1E:EC=1:2.