题目内容
(Ⅰ)求以点F1(-2,0),F2(2,0)分别为左右焦点,且经过点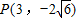 的椭圆的标准方程;
的椭圆的标准方程;(Ⅱ)求与双曲线
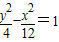 有相同渐近线,且经过点
有相同渐近线,且经过点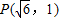 的双曲线的标准方程.
的双曲线的标准方程.
【答案】分析:(Ⅰ)设椭圆方程,利用点F1(-2,0),F2(2,0)分别为左右焦点,且经过点 ,建立方程组,求出几何量,即可得到椭圆的标准方程;
,建立方程组,求出几何量,即可得到椭圆的标准方程;
(Ⅱ)设双曲线方程为 ,代入P的坐标,即可得到双曲线的标准方程.
,代入P的坐标,即可得到双曲线的标准方程.
解答:解:(Ⅰ)设椭圆方程为 (a>b>0),则
(a>b>0),则
∴a2=36,b2=32
∴椭圆方程为 ;
;
(Ⅱ)设双曲线方程为
将点 代入双曲线方程,可得
代入双曲线方程,可得
∴λ=-
∴双曲线方程为 ,即
,即 .
.
点评:本题考查椭圆、双曲线的标准方程,考查待定系数法的运用,属于中档题.
 ,建立方程组,求出几何量,即可得到椭圆的标准方程;
,建立方程组,求出几何量,即可得到椭圆的标准方程;(Ⅱ)设双曲线方程为
 ,代入P的坐标,即可得到双曲线的标准方程.
,代入P的坐标,即可得到双曲线的标准方程.解答:解:(Ⅰ)设椭圆方程为
 (a>b>0),则
(a>b>0),则
∴a2=36,b2=32
∴椭圆方程为
 ;
;(Ⅱ)设双曲线方程为

将点
 代入双曲线方程,可得
代入双曲线方程,可得
∴λ=-

∴双曲线方程为
 ,即
,即 .
.点评:本题考查椭圆、双曲线的标准方程,考查待定系数法的运用,属于中档题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
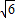 )的椭圆的标准方程;
)的椭圆的标准方程;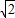 ,且经过点P(4,-
,且经过点P(4,-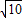 )的双曲线的方程.
)的双曲线的方程.