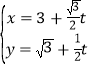题目内容
【题目】已知函数![]() ,
,![]() 为实数.
为实数.
(1)当![]() 时,求
时,求![]() 的最小值
的最小值![]() ;
;
(2)若存在实数![]() ,使得对任意实数
,使得对任意实数![]() 都有
都有![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
【答案】(1)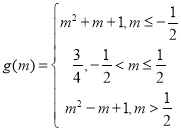 ;(2)
;(2)![]()
【解析】
(1)根据题意将二次函数配成顶点式,画出函数图像.通过对![]() 分类讨论,即可确定在不同区间内的最小值.
分类讨论,即可确定在不同区间内的最小值.
(2)根据函数解析式,代入求得![]() ,再代入不等式中可得关于
,再代入不等式中可得关于![]() 的二次不等式
的二次不等式![]() .构造函数
.构造函数![]() ,即分析
,即分析![]() 对任意实数
对任意实数![]() 成立即可.由二次函数性质可知需满足
成立即可.由二次函数性质可知需满足![]() .得不等式组后,可利用
.得不等式组后,可利用![]() 求得
求得![]() 的取值范围.则
的取值范围.则![]() 在此范围内有解即可.构造函数
在此范围内有解即可.构造函数![]() ,即在
,即在![]() 时
时![]() 有解即可.根据二次函数的对称、与y轴交点情况,分类讨论即可求得n的取值范围.
有解即可.根据二次函数的对称、与y轴交点情况,分类讨论即可求得n的取值范围.
(1)函数![]()
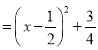
对应函数图像如下图所示:
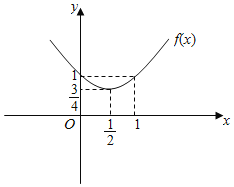
(ⅰ)当![]() 即
即![]() 时,
时,![]() ,
,
(ⅱ)当![]() 即
即![]() 时,
时,![]() ,
,
(ⅲ)当![]() 时,
时,![]() .
.
综上,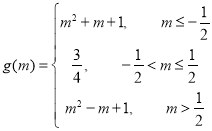
(2)因为![]()
则![]()
因为![]()
代入得![]() ,变形可得
,变形可得![]()
令![]() ,即对任意实数
,即对任意实数![]() ,
,![]() 成立
成立
由二次函数性质可得![]() ,代入可得
,代入可得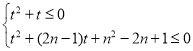
![]() 关于t的不等式组
关于t的不等式组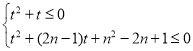 有解即可,
有解即可,
解不等式![]() 可得
可得![]()
![]() 在
在![]() 上有解即可
上有解即可
令![]()
因为![]() ,所以
,所以![]() ,所以函数
,所以函数![]() 与y轴交点位于y轴正半轴
与y轴交点位于y轴正半轴
(ⅰ)当对称轴位于![]() 左侧时,满足
左侧时,满足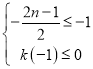 即可,也就是
即可,也就是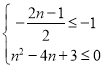 ,解不等式组可得
,解不等式组可得![]() ,
,
(ⅱ)当对称轴位于![]() 之间时,满足
之间时,满足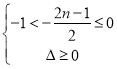 即可,也就是
即可,也就是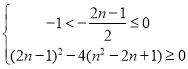 ,解得
,解得![]()
(ⅲ)当对称轴在![]() 右侧时,即
右侧时,即 ![]() 时,函数
时,函数![]() 在
在![]() 时无解.
时无解.
综上可知![]()
又因为![]() ,
,
∴n的取值范围是![]()

【题目】已知函数![]() .
.
(1)完成表一中![]() 对应的
对应的![]() 值,并在坐标系中用描点法作出函数
值,并在坐标系中用描点法作出函数![]() 的图象:(表一)
的图象:(表一)
| 0.25 | 0.5 | 0.75 | 1 | 1.25 | 1.5 |
| 0.08 | 1.82 | 2.58 |
(2)根据你所作图象判断函数![]() 的单调性,并用定义证明;
的单调性,并用定义证明;
(3)说明方程![]() 的根在区间
的根在区间![]() 存在的理由,并从表二中求使方程
存在的理由,并从表二中求使方程![]() 的根的近似值达到精确度为0.01时运算次数
的根的近似值达到精确度为0.01时运算次数![]() 的最小值并求此时方程
的最小值并求此时方程![]() 的根的近似值,且说明理由.
的根的近似值,且说明理由.
(表二)二分法的结果
运算次数 |
| 左端点 | 右端点 |
|
| -0.537 | 0.6 | 0.75 | 0.08 |
| -0.217 | 0.675 | 0.75 | 0.08 |
| -0.064 | 0.7125 | 0.75 | 0.08 |
| -0.064 | 0.7125 | 0.73125 | 0.011 |
| -0.03 | 0.721875 | 0.73125 | 0.011 |
| -0.01 | 0.7265625 | 0.73125 | 0.011 |