题目内容
定义在
上的偶函数
满足：对任意的
，有
，则（ ）
A． | B． |
C． | D． |
A
解析试题分析：由已知可知当时，
与
的符号相反，既
时
；
时
，所以函数在
上为减函数，又函数为偶函数，所以
，而
，所以
即，答案选A．
考点：函数的性质与应用
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
命题“
，
”的否定是（ ）
A．, | B． , |
C．， | D．， |
若
，则
（ ）
A． | B． | C． | D． |
若
，则
（ ）
| A．2 | B．2或-2 | C． | D．-2 |
下列各组函数是同一函数的是（ ）
①
与
；
②
与
；
③
与
；
④
与
．
| A．①②③ | B．②③④ | C．①③④ | D．①②④ |
函数
的定义域为（ ）
A． | B． | C． | D． |
（ ）
A． | B． | C． | D．18 |
设
,若
是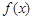
的最小值,则
的取值范围为（ ）
| A．[-1,2] | B．[-1,0] | C．[1,2] | D．[0,2] |
函数
为偶函数，且
上单调递减，则
的一个单调递增区间为（ ）
A． | B． | C． | D． |