题目内容
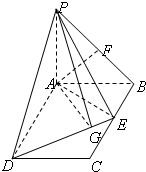 如图:PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成角是30°,点F是PB的中点,点E在边BC上移动.
如图:PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成角是30°,点F是PB的中点,点E在边BC上移动.(1)点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(2)无论点E在边BC的何处,PE与AF所成角是否都为定值,若是,求出其大小;若不是,请说明理由;
(3)当BE等于何值时,二面角P-DE-A的大小为45°.
分析:解法一(几何法):(1)线与面的位置关系有三种相交、平行与在面内,由题设中的条件E,F为中点可得EF∥PC,由此可判断出EF与平面PAC的位置关系是平行,再由线面平行的判定定理证明说明理由;
(2)由题设条件及图形可得出AF⊥平面PBE,由线面垂直的定义可得出无论点E在边BC的何处两线都垂直.
(3)先作出二面角的平面角,令其大小是45°,设BE=x,在直角三角形DCE中用勾股定理建立方程求同x值.
解法二(向量法):(1)的解法同法一中(1)的解法;
(2)建立如图示空间直角坐标系,由ABCD是矩形,PA=AB=1,PD与平面ABCD所成角是30°,点F是PB的中点,点E在边BC上移动,给出各点的坐标,求出PE与AF所对应的向量的坐标,验证其内积为0即可得出直线所成的角是直角;
(3)先求出两平面的法向量,再由公式求出两个平面的夹角.
(2)由题设条件及图形可得出AF⊥平面PBE,由线面垂直的定义可得出无论点E在边BC的何处两线都垂直.
(3)先作出二面角的平面角,令其大小是45°,设BE=x,在直角三角形DCE中用勾股定理建立方程求同x值.
解法二(向量法):(1)的解法同法一中(1)的解法;
(2)建立如图示空间直角坐标系,由ABCD是矩形,PA=AB=1,PD与平面ABCD所成角是30°,点F是PB的中点,点E在边BC上移动,给出各点的坐标,求出PE与AF所对应的向量的坐标,验证其内积为0即可得出直线所成的角是直角;
(3)先求出两平面的法向量,再由公式求出两个平面的夹角.
解答: 解:解法一:(1)当点E为BC的中点时,EF与平面PAC平行.
解:解法一:(1)当点E为BC的中点时,EF与平面PAC平行.
∵在△PBC中,E、F分别为BC、PB的中点,∴EF∥PC又EF?平面PAC
而PC?平面PAC∴EF∥平面PAC.
(2)∵PA⊥平面ABCD,BE?平面ABCD,∴EB⊥PA.又EB⊥AB,AB∩AP=A,AB,AP?平面PAB,∴EB⊥平面PAB,
又AF?平面PAB,∴AF⊥BE.
又PA=AB=1,点F是PB的中点,∴AF⊥PB,又∵PB∩BE=B,PB,BE?平面PBE,∴AF⊥平面PBE.
∵PE?平面PBE,∴AF⊥PE.即无论点E在边BC的何处,
PE与AF所成角都是定值90°.
(3)过A作AG⊥DE于G,连PG,又∵DE⊥PA,
则DE⊥平面PAG,
则∠PGA是二面角P-DE-A的平面角,
∴∠PGA=45°,
∵PD与平面ABCD所成角是30°,∴∠PDA=30°,
∴AD=
,PA=AB=1.
∴AG=1,DG=
,设BE=x,则GE=x,CE=
-x,
在Rt△DCE中,(
+x)2=(
-x)2+12,BE=x=
-
.
解法二:(向量法)(1)同解法一
(2)建立图示空间直角坐标系,则P(0,0,1),B(0,1,0),F(0,
,
),D(
,0,0).
设BE=x,则E(x,1,0)
-
=(x,1,-1)•(0,
,
)=0
∴AF⊥PE即PE与AF所成角是定值90°
(3)设平面PDE的法向量为
=(p,q,1),由
,得:
=(
,1-
,1),而平面ADE的法向量为
=(0,0,1),
∵二面角P-DE-A的大小是45°,所以cos45°=
=
,
∴
=
,
得BE=x=
-
或 BE=x=
+
(舍).
 解:解法一:(1)当点E为BC的中点时,EF与平面PAC平行.
解:解法一:(1)当点E为BC的中点时,EF与平面PAC平行.∵在△PBC中,E、F分别为BC、PB的中点,∴EF∥PC又EF?平面PAC
而PC?平面PAC∴EF∥平面PAC.
(2)∵PA⊥平面ABCD,BE?平面ABCD,∴EB⊥PA.又EB⊥AB,AB∩AP=A,AB,AP?平面PAB,∴EB⊥平面PAB,
又AF?平面PAB,∴AF⊥BE.
又PA=AB=1,点F是PB的中点,∴AF⊥PB,又∵PB∩BE=B,PB,BE?平面PBE,∴AF⊥平面PBE.
∵PE?平面PBE,∴AF⊥PE.即无论点E在边BC的何处,
PE与AF所成角都是定值90°.
(3)过A作AG⊥DE于G,连PG,又∵DE⊥PA,
则DE⊥平面PAG,
则∠PGA是二面角P-DE-A的平面角,
∴∠PGA=45°,
∵PD与平面ABCD所成角是30°,∴∠PDA=30°,
∴AD=
| 3 |
∴AG=1,DG=
| 2 |
| 3 |
在Rt△DCE中,(
| 2 |
| 3 |
| 3 |
| 2 |
解法二:(向量法)(1)同解法一

(2)建立图示空间直角坐标系,则P(0,0,1),B(0,1,0),F(0,
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
设BE=x,则E(x,1,0)
| PE |
| AF |
| 1 |
| 2 |
| 1 |
| 2 |
∴AF⊥PE即PE与AF所成角是定值90°
(3)设平面PDE的法向量为
| m |
|
| m |
| 1 | ||
|
| x | ||
|
| AP |
∵二面角P-DE-A的大小是45°,所以cos45°=
| ||
| 2 |
|
| ||||
|
|
∴
| 1 | ||||||||
|
| 1 | ||
|
得BE=x=
| 3 |
| 2 |
| 3 |
| 2 |
点评:本题考查空间向量求两平面的夹角,解题的关键是理解并掌握用空间向量求两平面夹角的方法,近几年高中数学引入空间向量,大大降低了立体几何中点线面间关系判断的思维含量,降低了难度,使得抽象的几何问题变成了简明的代数计算,用向量示解几何问题的一般步骤是:先根据图形的结构建立适当的坐标系,给出各点的坐标,如果研究两线的位置关系问题,可以求出两向量的方向向量,用公式求夹角,若研究线面夹角问题可求出线的方向向量与面的法向量,由公式求角,若研究两面的夹角问题,可求出两面的法向量,由公式求夹角.

练习册系列答案
相关题目
 如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,M,N分别是AB,PC的中点.
如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,M,N分别是AB,PC的中点. 如图,PA⊥平面AC,四边形ABCD是矩形,E、F分别是AB、PD的中点.
如图,PA⊥平面AC,四边形ABCD是矩形,E、F分别是AB、PD的中点. 如图,PA⊥平面ABC,AC⊥BC,AB=2,
如图,PA⊥平面ABC,AC⊥BC,AB=2, (2010•天津模拟)如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点
(2010•天津模拟)如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点 如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点F是PB的中点,点E在边BC上移动.
如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点F是PB的中点,点E在边BC上移动.