题目内容
(本题满分12分)某项竞赛分别为初赛、复赛、决赛三个阶段进行,每个阶段选手要
回答一个问题.规定正确回答问题者进入下一阶段竞赛,否则即遭淘汰.已知某选手通过初赛、复赛、决赛的概率分别是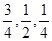 ,且各阶段通过与否相互独立.
,且各阶段通过与否相互独立.
(1)求该选手在复赛阶段被淘汰的概率;
(2)设该选手在竞赛中回答问题的个数为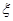 ,求
,求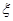 的分布列、数学期望和方差.
的分布列、数学期望和方差.
【答案】
(1)该选手在复赛阶段被淘汰的概率

(2) 的分布列为:
的分布列为:
|
|
1 |
2 |
3 |
|
P |
|
|
|
 的数学期望
的数学期望

 的方差
的方差

【解析】解:(1)记“该选手通过初赛”为事件A,“该选手通过复赛”为事件B,“该选手通过
决赛”为事件C,则

那么该选手在复赛阶段被淘汰的概率
 .
-------6分
.
-------6分
(2) 可能取值为1,2,3.
-------7分
可能取值为1,2,3.
-------7分

 的分布列为:
的分布列为:
|
|
1 |
2 |
3 |
|
P |
|
|
|
-------10分
 的数学期望
的数学期望
 -------11分
-------11分
 的方差
的方差
 .-------12分
.-------12分

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目


 ,
, ,…,
,…, 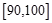 后得到如下频率分布直方图.
后得到如下频率分布直方图.
 内的频率;
内的频率; 两型会议桌,每套会议桌需经过加工木材和上油漆两道工序才能完成。已知做一套
两型会议桌,每套会议桌需经过加工木材和上油漆两道工序才能完成。已知做一套 的厂房(不管墙高),工程的造价是:
的厂房(不管墙高),工程的造价是: