题目内容
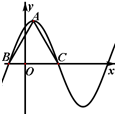
函数f(x)=6cos2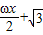 sinωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形.
sinωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形.(Ⅰ)求ω的值及函数f(x)的值域;
(Ⅱ)若f(x)=
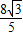 ,且x∈(-
,且x∈(-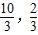 ),求f(x+1)的值.
),求f(x+1)的值.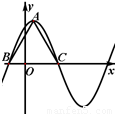
【答案】分析:(Ⅰ)将f(x)化简为f(x)=2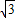 sin(ωx+
sin(ωx+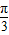 ),利用正弦函数的周期公式与性质可求ω的值及函数f(x)的值域;
),利用正弦函数的周期公式与性质可求ω的值及函数f(x)的值域;
(Ⅱ)由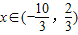 ,知
,知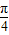 x+
x+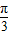 ∈(-
∈(-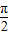 ,
,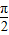 ),由
),由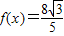 ,可求得即sin(
,可求得即sin(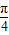 x+
x+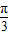 )=
)= ,利用两角和的正弦公式即可求得f(x+1).
,利用两角和的正弦公式即可求得f(x+1).
解答:解:(Ⅰ)由已知可得,f(x)=3cosωx+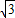 sinωx
sinωx
=2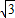 sin(ωx+
sin(ωx+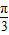 ),
),
又正三角形ABC的高为2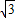 ,从而BC=4,
,从而BC=4,
∴函数f(x)的周期T=4×2=8,即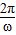 =8,ω=
=8,ω=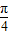 ,
,
∴数f(x)的值域为[-2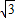 ,2
,2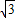 ]…6分
]…6分
(Ⅱ)∵f(x)=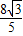 ,由(Ⅰ)有f(x)=2
,由(Ⅰ)有f(x)=2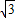 sin(
sin(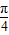 x+
x+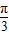 )=
)=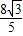 ,
,
即sin(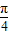 x+
x+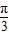 )=
)= ,由
,由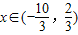 ,知
,知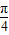 x+
x+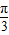 ∈(-
∈(-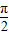 ,
,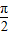 ),
),
∴cos(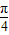 x+
x+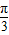 )=
)=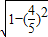 =
= .
.
∴f(x+1)=2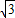 sin(
sin(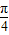 x+
x+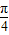 +
+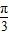 )=2
)=2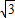 sin[(
sin[(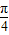 x+
x+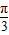 )+
)+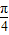 ]=2
]=2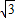 [sin(
[sin(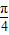 x+
x+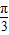 )cos
)cos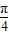 +cos(
+cos(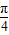 x+
x+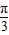 )sin
)sin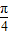 ]
]
=2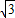 (
( ×
×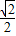 +
+ ×
×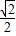 )
)
=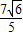 …12分
…12分
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,着重考查三角函数的化简求值与正弦函数的性质,考查分析转化与运算能力,属于中档题.
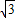 sin(ωx+
sin(ωx+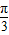 ),利用正弦函数的周期公式与性质可求ω的值及函数f(x)的值域;
),利用正弦函数的周期公式与性质可求ω的值及函数f(x)的值域;(Ⅱ)由
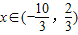 ,知
,知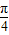 x+
x+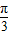 ∈(-
∈(-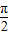 ,
,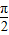 ),由
),由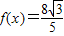 ,可求得即sin(
,可求得即sin(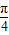 x+
x+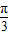 )=
)= ,利用两角和的正弦公式即可求得f(x+1).
,利用两角和的正弦公式即可求得f(x+1).解答:解:(Ⅰ)由已知可得,f(x)=3cosωx+
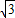 sinωx
sinωx=2
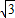 sin(ωx+
sin(ωx+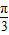 ),
),又正三角形ABC的高为2
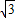 ,从而BC=4,
,从而BC=4,∴函数f(x)的周期T=4×2=8,即
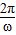 =8,ω=
=8,ω=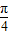 ,
,∴数f(x)的值域为[-2
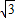 ,2
,2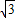 ]…6分
]…6分(Ⅱ)∵f(x)=
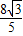 ,由(Ⅰ)有f(x)=2
,由(Ⅰ)有f(x)=2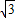 sin(
sin(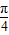 x+
x+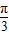 )=
)=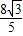 ,
,即sin(
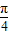 x+
x+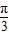 )=
)= ,由
,由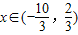 ,知
,知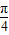 x+
x+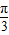 ∈(-
∈(-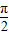 ,
,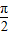 ),
),∴cos(
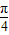 x+
x+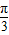 )=
)=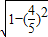 =
= .
.∴f(x+1)=2
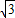 sin(
sin(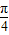 x+
x+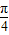 +
+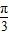 )=2
)=2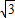 sin[(
sin[(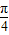 x+
x+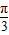 )+
)+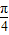 ]=2
]=2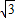 [sin(
[sin(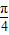 x+
x+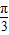 )cos
)cos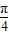 +cos(
+cos(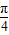 x+
x+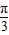 )sin
)sin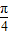 ]
]=2
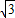 (
( ×
×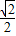 +
+ ×
×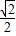 )
)=
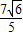 …12分
…12分点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,着重考查三角函数的化简求值与正弦函数的性质,考查分析转化与运算能力,属于中档题.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
 (2012•四川)函数f(x)=6cos2
(2012•四川)函数f(x)=6cos2 已知函数
已知函数