题目内容
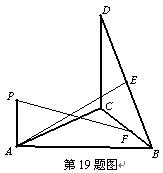
如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E为DB的中点。

(1)证明:AE⊥BC;
(2)若点F是线段BC上的动点,设面PFE与面PBE所成的平面角大小为 ,当
,当 在
在 内取值时,求直线PF与平面DBC所成的角的范围。
内取值时,求直线PF与平面DBC所成的角的范围。
(2)若点F是线段BC上的动点,设面PFE与面PBE所成的平面角大小为
 ,当
,当 在
在 内取值时,求直线PF与平面DBC所成的角的范围。
内取值时,求直线PF与平面DBC所成的角的范围。 (1)证明:取BC的中点O,连接EO,AO,则EO//DC,
所以EO⊥BC,
因为△ABC为等边三角形,所以BC⊥AO,
所以BC⊥面AEO,
故BC⊥AE。
(2)解:连接PE,
因为面BCD⊥面ABC,DC⊥BC,
所以DC⊥面ABC,
而EO
 DC,
DC,
所以EO PA,故四边形APEO为矩形,
PA,故四边形APEO为矩形,
易证PE⊥面BCD,
连接EF,则∠PFE为PF与面DBC所成的角,
又PE⊥面BCD,
所以 ,
,
∴∠BEF为面PBE与面PFE所成的角,即 ,
,
此时点F即在线段BO上移动,设DC=BC=2PA=2,则 ,
,
 ,
,
所以直线PF与平面DBC所成的角的范围为 。
。
所以EO⊥BC,
因为△ABC为等边三角形,所以BC⊥AO,
所以BC⊥面AEO,
故BC⊥AE。
(2)解:连接PE,
因为面BCD⊥面ABC,DC⊥BC,
所以DC⊥面ABC,
而EO

 DC,
DC,所以EO
 PA,故四边形APEO为矩形,
PA,故四边形APEO为矩形,易证PE⊥面BCD,
连接EF,则∠PFE为PF与面DBC所成的角,
又PE⊥面BCD,
所以
 ,
, ∴∠BEF为面PBE与面PFE所成的角,即
 ,
,此时点F即在线段BO上移动,设DC=BC=2PA=2,则
 ,
, ,
,所以直线PF与平面DBC所成的角的范围为
 。
。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
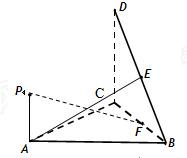 如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E为DB的中点.
如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E为DB的中点.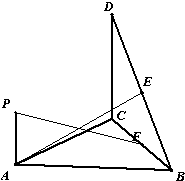 如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E、F分别为DB、CB的中点,
如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E、F分别为DB、CB的中点, (2010•温州一模)如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,为DB的中点,
(2010•温州一模)如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,为DB的中点,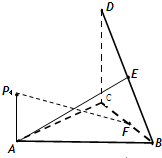 (2012•汕头一模)如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E为DB的中点.
(2012•汕头一模)如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E为DB的中点. ,
,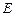 为DB的中点,
为DB的中点,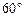 ,若存在,试确定点F的位置,若不存在,说明理由.
,若存在,试确定点F的位置,若不存在,说明理由.