题目内容
设二次函数f(x)=ax2+bx+c(a,b,c∈R,a≠0)满足条件:
(1)当x∈R时,f(x-4)=f(2-x),且f(x)≥x:
(2)当x∈(0,2)时,f(x)≤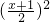 ;
;
(3)f(x)在R上的最小值为0.
求最大的m(m>1),使得存在t∈R,只要x∈[1,m],就有f(x+t)≤x.
解:因f(x-4)=f(2-x),则函数的图象关于x=-1对称,∴ =-1,b=2a,
=-1,b=2a,
由(3),x=-1时,y=0,即a-b+c=0,由(1)得,f(1)≥1,由(2)得,f(1)≤1,
则f(1)=1,即a+b+c=1.又a-b+c=0,则b= ,a=
,a= ,c=
,c= ,故f(x)=
,故f(x)= x2+
x2+ x+
x+ .
.
假设存在t∈R,只要x∈[1,m],就有f(x+t)≤x.
取x=1,有f(t+1)≤1,即 (t+1)2+
(t+1)2+ (t+1)+
(t+1)+ ≤1,解得-4≤t≤0,
≤1,解得-4≤t≤0,
对固定的t∈[-4,0],取x=m,有f(t+m)≤m,即 (t+m)2+
(t+m)2+ (t+m)+
(t+m)+ ≤m.
≤m.
化简有:m2-2(1-t)m+(t2+2t+1)≤0,解得1-t-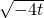 ≤m≤1-t+
≤m≤1-t+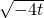 ,
,
故m≤1-t-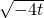 ≤1-(-4)+
≤1-(-4)+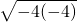 =9
=9
当t=-4时,对任意的x∈[1,9],
恒有f(x-4)-x= (x2-10x+9)=
(x2-10x+9)= (x-1)(x-9)≤0.
(x-1)(x-9)≤0.
∴m的最大值为9.
解:∵f(x-4)=f(2-x)
∴函数的图象关于x=-1对称
∴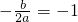 b=2a
b=2a
由③知当x=-1时,y=0,即a-b+c=0
由①得 f(1)≥1,由②得 f(1)≤1
∴f(1)=1,即工+了+以=1,又a-b+c=0
∴a= b=
b= c=
c=
∴f(x)=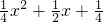 …
…
假设存在t∈R,只要x∈[1,m],就有f(x+t)≤x
取x=1时,有f(t+1)≤1? (t+1)2+
(t+1)2+ (t+1)+
(t+1)+ ≤1?-4≤t≤0
≤1?-4≤t≤0
对固定的t∈[-4,0],取x=m,有
f(t+m)≤m? (t+m)2+
(t+m)2+ (t+m)+
(t+m)+ ≤m?m2-2(1-t)m+(t2+2t+1)≤0?
≤m?m2-2(1-t)m+(t2+2t+1)≤0?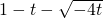 ≤m≤
≤m≤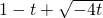 …
…
∴m≤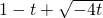 ≤
≤ =9 …
=9 …
当t=-4时,对任意的x∈[1,9],恒有
f(x-4)-x= (x2-10x+9)=
(x2-10x+9)= (x-1)(x-9)≤0
(x-1)(x-9)≤0
∴m的最大值为9. …
另解:∵f(x-4)=f(2-x)
∴函数的图象关于x=-1对称
∴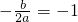 b=2a
b=2a
由③知当x=-1时,y=0,即a-b+c=0
由①得 f(1)≥1,由②得 f(1)≤1
∴f(1)=1,即工+了+以=1,又a-b+c=0
∴a= b=
b= c=
c=
∴f(x)=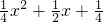 =
= (x+1)2 …
(x+1)2 …
由f(x+t)= (x+t+1)2≤x 在x∈[1,m]上恒成立
(x+t+1)2≤x 在x∈[1,m]上恒成立
∴4[f(x+t)-x]=x2+2(t-1)x+(t+1)2≤0当x∈[1,m]时,恒成立
令 x=1有t2+4t≤0?-4≤t≤0
令x=m有t2+2(m+1)t+(m-1)2≤0当t∈[-4,0]时,恒有解 …
令t=-4得,m2-10m+9≤0?1≤m≤9 …
即当t=-4时,任取x∈[1,9]恒有
f(x-4)-x= (x2-10x+9)=
(x2-10x+9)= (x-1)(x-9)≤0
(x-1)(x-9)≤0
∴mmax=9 …
分析:通过三个条件先求出函数解析式f(x)= x2+
x2+ x+
x+ ,只要x∈[1,m],就有f(x+t)≤x.那么当x=1时也成立确定出t的范围,然后研究当x=m时也应成立,利用函数的单调性求出m的最值.
,只要x∈[1,m],就有f(x+t)≤x.那么当x=1时也成立确定出t的范围,然后研究当x=m时也应成立,利用函数的单调性求出m的最值.
点评:本题考查了函数的最值问题,以及利用函数单调性进行求解最值,考查了学生的计算能力,属于中档题.
 =-1,b=2a,
=-1,b=2a,由(3),x=-1时,y=0,即a-b+c=0,由(1)得,f(1)≥1,由(2)得,f(1)≤1,
则f(1)=1,即a+b+c=1.又a-b+c=0,则b=
 ,a=
,a= ,c=
,c= ,故f(x)=
,故f(x)= x2+
x2+ x+
x+ .
.假设存在t∈R,只要x∈[1,m],就有f(x+t)≤x.
取x=1,有f(t+1)≤1,即
 (t+1)2+
(t+1)2+ (t+1)+
(t+1)+ ≤1,解得-4≤t≤0,
≤1,解得-4≤t≤0,对固定的t∈[-4,0],取x=m,有f(t+m)≤m,即
 (t+m)2+
(t+m)2+ (t+m)+
(t+m)+ ≤m.
≤m.化简有:m2-2(1-t)m+(t2+2t+1)≤0,解得1-t-
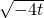 ≤m≤1-t+
≤m≤1-t+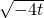 ,
,故m≤1-t-
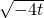 ≤1-(-4)+
≤1-(-4)+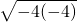 =9
=9当t=-4时,对任意的x∈[1,9],
恒有f(x-4)-x=
 (x2-10x+9)=
(x2-10x+9)= (x-1)(x-9)≤0.
(x-1)(x-9)≤0.∴m的最大值为9.
解:∵f(x-4)=f(2-x)
∴函数的图象关于x=-1对称
∴
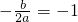 b=2a
b=2a由③知当x=-1时,y=0,即a-b+c=0
由①得 f(1)≥1,由②得 f(1)≤1
∴f(1)=1,即工+了+以=1,又a-b+c=0
∴a=
 b=
b= c=
c=
∴f(x)=
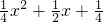 …
…假设存在t∈R,只要x∈[1,m],就有f(x+t)≤x
取x=1时,有f(t+1)≤1?
 (t+1)2+
(t+1)2+ (t+1)+
(t+1)+ ≤1?-4≤t≤0
≤1?-4≤t≤0对固定的t∈[-4,0],取x=m,有
f(t+m)≤m?
 (t+m)2+
(t+m)2+ (t+m)+
(t+m)+ ≤m?m2-2(1-t)m+(t2+2t+1)≤0?
≤m?m2-2(1-t)m+(t2+2t+1)≤0?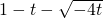 ≤m≤
≤m≤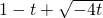 …
…∴m≤
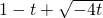 ≤
≤ =9 …
=9 …当t=-4时,对任意的x∈[1,9],恒有
f(x-4)-x=
 (x2-10x+9)=
(x2-10x+9)= (x-1)(x-9)≤0
(x-1)(x-9)≤0∴m的最大值为9. …
另解:∵f(x-4)=f(2-x)
∴函数的图象关于x=-1对称
∴
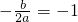 b=2a
b=2a由③知当x=-1时,y=0,即a-b+c=0
由①得 f(1)≥1,由②得 f(1)≤1
∴f(1)=1,即工+了+以=1,又a-b+c=0
∴a=
 b=
b= c=
c=
∴f(x)=
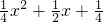 =
= (x+1)2 …
(x+1)2 …由f(x+t)=
 (x+t+1)2≤x 在x∈[1,m]上恒成立
(x+t+1)2≤x 在x∈[1,m]上恒成立∴4[f(x+t)-x]=x2+2(t-1)x+(t+1)2≤0当x∈[1,m]时,恒成立
令 x=1有t2+4t≤0?-4≤t≤0
令x=m有t2+2(m+1)t+(m-1)2≤0当t∈[-4,0]时,恒有解 …
令t=-4得,m2-10m+9≤0?1≤m≤9 …
即当t=-4时,任取x∈[1,9]恒有
f(x-4)-x=
 (x2-10x+9)=
(x2-10x+9)= (x-1)(x-9)≤0
(x-1)(x-9)≤0∴mmax=9 …
分析:通过三个条件先求出函数解析式f(x)=
 x2+
x2+ x+
x+ ,只要x∈[1,m],就有f(x+t)≤x.那么当x=1时也成立确定出t的范围,然后研究当x=m时也应成立,利用函数的单调性求出m的最值.
,只要x∈[1,m],就有f(x+t)≤x.那么当x=1时也成立确定出t的范围,然后研究当x=m时也应成立,利用函数的单调性求出m的最值.点评:本题考查了函数的最值问题,以及利用函数单调性进行求解最值,考查了学生的计算能力,属于中档题.

练习册系列答案
相关题目
设二次函数f(x)=ax2+bx+c(a>0),方程f(x)-x=0的两个根x1、x2满足0<x1<x2<
,且函数f(x)的图象关于直线x=x0对称,则有( )
| 1 |
| a |
A、x0≤
| ||
B、x0>
| ||
C、x0<
| ||
D、x0≥
|