题目内容
(本题满分18分)如果函数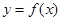 的定义域为
的定义域为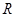 ,对于定义域内的任意
,对于定义域内的任意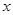 ,存在实数
,存在实数 使得
使得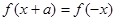 成立,则称此函数具有“
成立,则称此函数具有“ 性质”.
性质”.
(1)判断函数 是否具有“
是否具有“ 性质”,若具有“
性质”,若具有“ 性质”求出所有
性质”求出所有 的值;若不具有“
的值;若不具有“ 性质”,请说明理由.
性质”,请说明理由.
(2)已知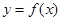 具有“
具有“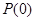 性质”,且当
性质”,且当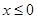 时
时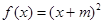 ,求
,求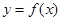 在
在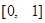 上的最大值.
上的最大值.
(3)设函数 具有“
具有“ 性质”,且当
性质”,且当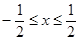 时,
时,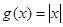 .若
.若 与
与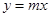 交点个数为2013个,求
交点个数为2013个,求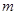 的值.
的值.
【答案】
(1) 具有“
具有“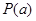 性质”,其中
性质”,其中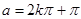
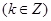
(2)当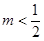 时,
时, 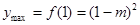 ;当
;当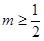 时,
时,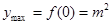
(3)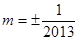
【解析】
试题分析:(1)由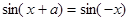 得
得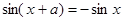 ,
,
根据诱导公式得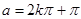
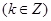 .
.
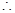
 具有“
具有“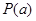 性质”,其中
性质”,其中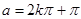
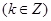 . ……4分
. ……4分
(2)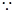
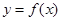 具有“
具有“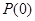 性质”,
性质”,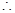
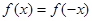 .
.
设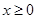 ,则
,则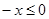 ,
,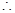
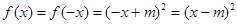
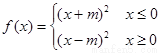 , ……6分
, ……6分
当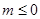 时,
时,
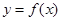 在
在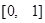 递增,
递增,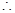
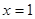 时
时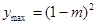 ,
,
当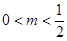 时,
时,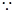
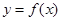 在
在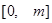 上递减,在
上递减,在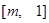 上递增,且
上递增,且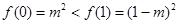 ,
, 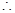
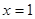 时
时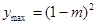 ,
,
当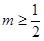 时,
时,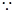
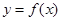 在
在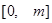 上递减,在
上递减,在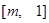 上递增,且
上递增,且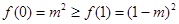 ,
,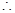
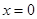 时
时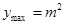
综上所述:
当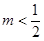 时,
时, 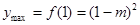 ;当
;当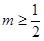 时,
时,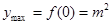 . ……11分
. ……11分
(3)
 具有“
具有“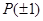 性质”,
性质”,
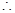
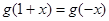 ,
,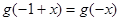 ,
,
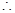
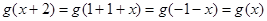 ,
,
从而得到 是以2为周期的函数.
是以2为周期的函数.
又设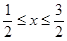 ,则
,则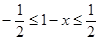 ,
,
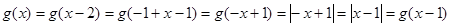 .
.
再设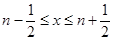 (
( ),
),
当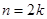 (
(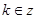 ),
),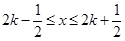 则
则 ,
,
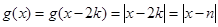 ;
;
当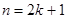 (
(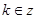 ),
),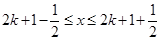 则
则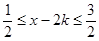 ,
,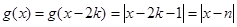 ;
;
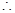 对于,
对于,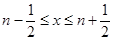 (
( ),都有
),都有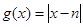 ,而
,而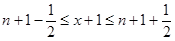 ,
,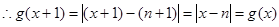 ,
,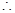
 是周期为1的函数.
是周期为1的函数.
①当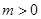 时,要使得
时,要使得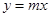 与
与 有2013个交点,只要
有2013个交点,只要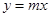 与
与 在
在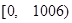 有2012个交点,而在
有2012个交点,而在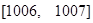 有一个交点.
有一个交点.
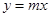 过
过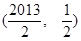 ,从而得
,从而得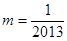
②当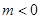 时,同理可得
时,同理可得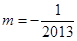
③当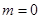 时,不合题意.
时,不合题意.
综上所述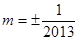 . ……18分
. ……18分
考点:本小题主要考查新定义下函数性质的考查,考查学生利用新定义解决问题的能力和分类讨论思想的应用.
点评:分类讨论解决问题时,要准确分类,分类标准要不重不漏,而且讨论完之后要讨论.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
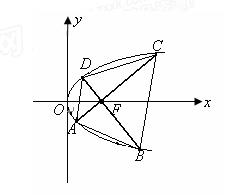
 )第一题满分5分,第二题满分5分,第三题满分8分.
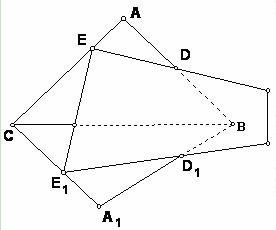
)第一题满分5分,第二题满分5分,第三题满分8分. 条交线ED,CB, E1 D1的关系。
条交线ED,CB, E1 D1的关系。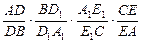 的值;
的值;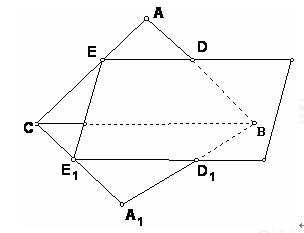
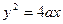 (
(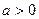 且
且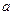 为常数),
为常数),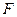 为其焦点.
为其焦点.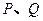 两点,且
两点,且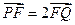 ,求直线
,求直线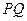 的斜率;
的斜率;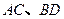 是过抛物线焦点
是过抛物线焦点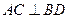 ,如图所示.求四边形
,如图所示.求四边形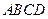 面积的最小值
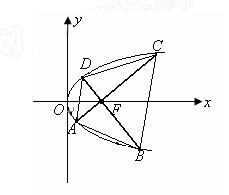
面积的最小值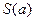 .
.
 开始依次水平向右和竖直向上跳动,其落点坐标依次是
开始依次水平向右和竖直向上跳动,其落点坐标依次是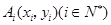 ,(如图所示,
,(如图所示, 坐标以已知条件为准),
坐标以已知条件为准), 表示青蛙从点
表示青蛙从点 到点
到点 所经过的路程。
所经过的路程。
 准线上
准线上 ,
, 均在该抛物线上,并且直线
均在该抛物线上,并且直线 .
.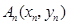 要么落在
要么落在 所表示的曲线上,
所表示的曲线上, 所表示的曲线上,并且
所表示的曲线上,并且 ,
, (不需证明);
(不需证明); 所表示的曲线上,要么落在
所表示的曲线上,要么落在 所表示的曲线上,并且
所表示的曲线上,并且 ,求
,求
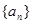 的前
的前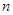 项和为
项和为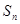 ,满足
,满足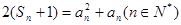 .
. 满足
满足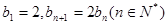 ,数列
,数列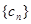 满足
满足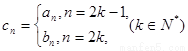 ,数列
,数列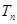 ,求
,求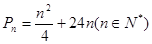 ,甲同学利用第(2)问中的
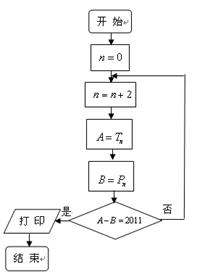
,甲同学利用第(2)问中的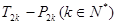 的值是否可以等于2011?为此,他设计了一个程序(如图),但乙同学认为这个程序如果被执行会是一个“死循环”(即程序会永远循环下去,而无法结束),你是否同意乙同学的观点?请说明理由.
的值是否可以等于2011?为此,他设计了一个程序(如图),但乙同学认为这个程序如果被执行会是一个“死循环”(即程序会永远循环下去,而无法结束),你是否同意乙同学的观点?请说明理由.