题目内容
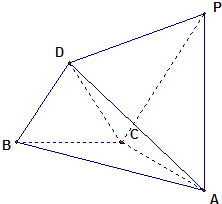 已知△ABC与△DBC都是边长为
已知△ABC与△DBC都是边长为2
| ||
| 3 |
(Ⅰ)求直线PD与平面ABC所成角的大小;
(Ⅱ)平面PDC与底面ABC所成的二面角的余弦值.
分析:(I)根据题意可知直线PD与平面ABC所成角就是直线PD与直线OA所成的角,过D作DM∥OA交PA于M,易知DO∥PA,从而求出∠PDM,即为所求;
(II)延长AO与PD的延长线交于点M,连接MC,过O向MC作OH⊥MC于M,连接DH,则∠OHD为所求二面角的平面角,然后在直角三角形OHD中求出此角即可.
(II)延长AO与PD的延长线交于点M,连接MC,过O向MC作OH⊥MC于M,连接DH,则∠OHD为所求二面角的平面角,然后在直角三角形OHD中求出此角即可.
解答: 解:(Ⅰ)∵D在平面ABC的射影是O,P在平面ABC的射影是A,
解:(Ⅰ)∵D在平面ABC的射影是O,P在平面ABC的射影是A,
∴DP在平面ABC的射影是OA,即直线PD与平面ABC所成角就是直线PD与直线OA所成的角,
过D作DM∥OA交PA于M,易知DO∥PA,
∴DM=OA=1,DO=MA=1?PM=1
∴cos∠PDM=
=
即∠PDM=45°
(Ⅱ)延长AO与PD的延长线交于点M,连接MC,过O向MC作OH⊥MC于M,连接DH,则∠OHD为所求二面角的平面角
∵DO=1,AO=1,MO=1,
∴HO=
=
=
cos∠OHD=
=
=
 解:(Ⅰ)∵D在平面ABC的射影是O,P在平面ABC的射影是A,
解:(Ⅰ)∵D在平面ABC的射影是O,P在平面ABC的射影是A,∴DP在平面ABC的射影是OA,即直线PD与平面ABC所成角就是直线PD与直线OA所成的角,
过D作DM∥OA交PA于M,易知DO∥PA,
∴DM=OA=1,DO=MA=1?PM=1
∴cos∠PDM=
| DM |
| PD |
| ||
| 2 |
即∠PDM=45°
(Ⅱ)延长AO与PD的延长线交于点M,连接MC,过O向MC作OH⊥MC于M,连接DH,则∠OHD为所求二面角的平面角
∵DO=1,AO=1,MO=1,

∴HO=
| MO•OC |
| MC |
1×
| ||||
|
| 1 |
| 2 |
| OH |
| DH |
| ||||
|
| ||
| 5 |
点评:本题主要考查了线面所成角的度量以及二面角平面角的度量,解题的关键是找出二面角的平面角,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD:DB=BE:EC=2:1,AE与CD交于P.设存在λ和μ使
如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD:DB=BE:EC=2:1,AE与CD交于P.设存在λ和μ使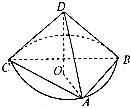 已知四面体ABCD中,DA=DB=DC=3
已知四面体ABCD中,DA=DB=DC=3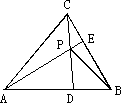
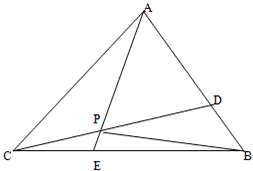 如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD:DB=BE:EC=2:1,AE与CD交于P.设存在λ和μ使
如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD:DB=BE:EC=2:1,AE与CD交于P.设存在λ和μ使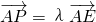 ,
,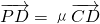 ,
,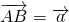 ,
,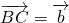 .
. ,
, 表示
表示 ;
;