题目内容
直线x=t(t>0)与函数f(x)=x2+1,g(x)=lnx的图象分别交于A、B两点,当|AB|最小时,t值是( )
分析:将两个函数作差,得到函数y=f(x)-g(x),再求此函数的最小值对应的自变量x的值.
解答:解:设函数y=f(x)-g(x)=x2-lnx+1,求导数得
y′=2x-
=
当0<x<
时,y′<0,函数在(0,
)上为单调减函数,
当x>
时,y′>0,函数在(
,+∞)上为单调增函数
所以当x=
时,所设函数的最小值为
+
ln2,
所求t的值为
.
故选B.
y′=2x-
| 1 |
| x |
| 2x2-1 |
| x |
当0<x<
| ||
| 2 |
| ||
| 2 |
当x>
| ||
| 2 |
| ||
| 2 |
所以当x=
| ||
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
所求t的值为
| ||
| 2 |
故选B.
点评:可以结合两个函数的草图,发现在(0,+∞)上x2>lnx恒成立,问题转化为求两个函数差的最小值对应的自变量x的值.

练习册系列答案
相关题目
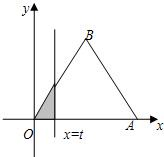 如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t).试求函数f(t)的解析式,并画出函数y=f(t)的图象.
如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t).试求函数f(t)的解析式,并画出函数y=f(t)的图象.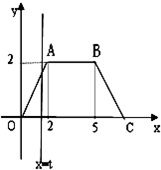 如图,在等腰梯形OABC中,A(2,2),B(5,2).直线x=t(t>0)由点O向点C移动,至点C完毕,记扫描梯形时所得直线x=t左侧的图形面积为f(t).试求f(t)的解析式,并画出y=f(t)的图象.
如图,在等腰梯形OABC中,A(2,2),B(5,2).直线x=t(t>0)由点O向点C移动,至点C完毕,记扫描梯形时所得直线x=t左侧的图形面积为f(t).试求f(t)的解析式,并画出y=f(t)的图象. 如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t).
如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t).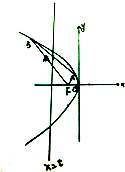 如图,A,B是焦点为F的抛物线y2=-4x上的两动点,线段AB的中点M在直线x=t(t<0)上.
如图,A,B是焦点为F的抛物线y2=-4x上的两动点,线段AB的中点M在直线x=t(t<0)上.