题目内容
(本小题满分14分)如图,直三棱柱 中,
中, ,
, ,棱
,棱 ,
, 、
、 分别是
分别是 、
、 的中点.
的中点.

(1)求证: 平面
平面 ;
;
(2)求直线 与平面
与平面 所成角
所成角 的正弦值.
的正弦值.
(1)见解析;(2) .
.
【解析】
试题分析:(1)证明: ,
, 底面,
底面,
 1分
1分
 ,
, 2分
2分
∵ ,
, ,
,
∴ 平面
平面 3分
3分
 4分
4分
又∵
∴ 平面
平面 6分
6分
(2)(方法一)以C为原点,CA、CB、CC1在直线分别为 轴、
轴、 轴、
轴、 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则 、
、 、
、 7分
7分
 、
、 8分
8分
 、
、 、
、 10分
10分
设平面 的一个法向为
的一个法向为 ,则
,则 11分
11分
即 ,取
,取 12分
12分
所以 13分
13分
 14分
14分
(方法二) ,
, ,
, 7分
7分
∴ ,
, ,
, 8分
8分
由(1)知 ,
, ,
,
∴ 平面
平面 9分
9分
延长 到
到 ,延长
,延长 到
到 ,使
,使 ,连接
,连接 、
、 10分
10分
在 中,
中, ,
, ,
, 11分
11分
∴ 12分
12分
 13分
13分
∵ 是平面
是平面 的法向量,由所作知
的法向量,由所作知 ,从而
,从而
∴ 14分
14分
考点:考查了直线与平面垂直的判定和直线与平面所成角.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目

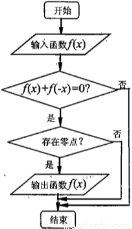
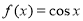 B.
B.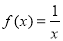
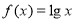 D.
D.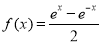
 ,
, ,
, ,
, ,满足
,满足 ,
,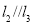 ,
, ,则下列结论一定正确的是( )
,则下列结论一定正确的是( )

 与
与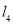 既不垂直也不平行
既不垂直也不平行  与
与 的位置关系不确定
的位置关系不确定 满足
满足 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
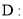
 ,令点集
,令点集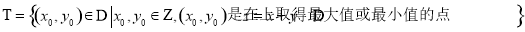 ,则
,则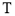 中的点共确定__________条不同的直线.
中的点共确定__________条不同的直线. ,
, 是两条不同的直线,
是两条不同的直线, ,
, 是两个不同的平面,下列命题中正确的是( )
是两个不同的平面,下列命题中正确的是( ) ,
, ,
, ,则
,则
 ,
, ,
, ,则
,则
 ,
, ,
, ,则
,则
 ,
, ,
, ,则
,则
 ( )
( )