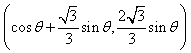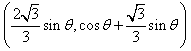题目内容
如图所示,点P在正方形ABCD所在平面外,PA⊥平面ABCD,PA=AB,则PB与AC所成的角是( )

A.90° B.60°
C.45° D.30°
【答案】
B
【解析】
试题分析:连接BD交AC于点O,取PD中点Q,连接OQ,所以OQ//PB,
设正方形ABCD边长为a,因为PA垂直平面ABCD,PA=AB,所以PD=PB=DB=AC= ,
,
因为在三角形DBP中,O、Q是中点,所以 ,在直角三角形PAD中,
,在直角三角形PAD中, , 而
, 而 ,所以三角形AOQ是等边三角形,即三个角都是60度,所以OQ与AC所成的角=60度, 因为OQ||PB,所以PB与AC所成的角为60°.
,所以三角形AOQ是等边三角形,即三个角都是60度,所以OQ与AC所成的角=60度, 因为OQ||PB,所以PB与AC所成的角为60°.
考点:本小题主要考查两条异面直线的夹角.
点评:要求两条异面直线的夹角,需要先做出两条异面直线的夹角再求解,注意两条异面直线的夹角的取值范围。

练习册系列答案
相关题目
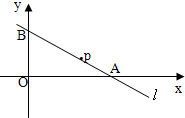 如图所示,直线l过点P(6,2),且和x轴,y轴正方向分别交于A,B两点,求直线l在两坐标轴上截距之和S的最小值及此时直线l的方程.
如图所示,直线l过点P(6,2),且和x轴,y轴正方向分别交于A,B两点,求直线l在两坐标轴上截距之和S的最小值及此时直线l的方程. (其中
(其中 分别是斜坐标系x轴、y轴正方向上的单位向量,x、y∈R,O为坐标原点),则有序实数对(x,y)称为点P的斜坐标.如图所示,在平面斜坐标系xOy中,若∠xOy=120°,点A(1,0),P为单位圆上一点,且∠AOP=
分别是斜坐标系x轴、y轴正方向上的单位向量,x、y∈R,O为坐标原点),则有序实数对(x,y)称为点P的斜坐标.如图所示,在平面斜坐标系xOy中,若∠xOy=120°,点A(1,0),P为单位圆上一点,且∠AOP=


 的概率P1;
的概率P1; 的概率P2。
的概率P2。
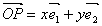 (其中
(其中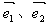 分别是斜坐标系x轴、y轴正方向上的单位向量,x、y∈R,O为坐标原点),则有序实数对(x,y)称为点P的斜坐标。如图所示,在平面斜坐标系xOy中,若∠xOy=120°,点A(1,0),P为单位圆上一点,且∠AOP=θ,点P在平面斜坐标系中的坐标是
分别是斜坐标系x轴、y轴正方向上的单位向量,x、y∈R,O为坐标原点),则有序实数对(x,y)称为点P的斜坐标。如图所示,在平面斜坐标系xOy中,若∠xOy=120°,点A(1,0),P为单位圆上一点,且∠AOP=θ,点P在平面斜坐标系中的坐标是