题目内容
把函数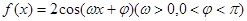 的图像上的每一点的横坐标伸长为原来的2倍,纵坐标不变,然后再向左平移
的图像上的每一点的横坐标伸长为原来的2倍,纵坐标不变,然后再向左平移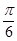 个单位后得到一个最小正周期为
个单位后得到一个最小正周期为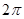 的奇函数
的奇函数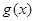 。
。
(1)求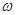 和
和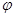 的值
的值
(2)求函数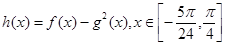 的最大值与最小值。
的最大值与最小值。
(1) ,
, (2)
(2)
解析试题分析:(1)将函数 的图像上的每一点的横坐标伸长为原来的2倍,纵坐标不变,然后再向左平移
的图像上的每一点的横坐标伸长为原来的2倍,纵坐标不变,然后再向左平移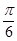 个单位后得到:
个单位后得到: 。
。
由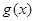 是最小正周期为
是最小正周期为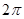 的奇函数得
的奇函数得 且
且 。又
。又 所以
所以 。
。
(2)由(1)知 ,所以
,所以 。
。 ,
,
考点:三角函数图像的平移伸缩变化及三角函数求最值
点评: 中A与y轴上的伸缩有关,B与y轴上的平移有关,
中A与y轴上的伸缩有关,B与y轴上的平移有关,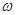 与x轴上的伸缩有关,
与x轴上的伸缩有关,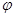 与x轴上的平移有关,求三角函数最值先要将其整理为
与x轴上的平移有关,求三角函数最值先要将其整理为 的形式,再结合定义域可求得值域最值
的形式,再结合定义域可求得值域最值

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
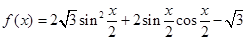 ,
,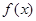 的单调递减区间;
的单调递减区间; 时,求函数
时,求函数 .
. 上的函数
上的函数 的图象关于直线
的图象关于直线 对称,当
对称,当 时,函数
时,函数 ,其图象如图
,其图象如图
 在
在 的表达式;
的表达式; 的解.
的解.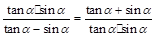 .
.
 的最小正周期;
的最小正周期; ,
,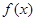 的最小值是
的最小值是 ,最大值是
,最大值是 ,求实数
,求实数 的值.
的值. 中,三个内角
中,三个内角 所对的边分别为
所对的边分别为 ,
, ,
,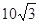 .
.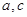 的值;(6分)
的值;(6分)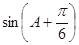 .(4分)
.(4分) .
.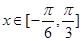 时,函数
时,函数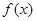 的最大值与最小值的和为
的最大值与最小值的和为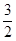 ,求
,求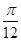 个单位,纵坐标不变横坐标变为原来的2
个单位,纵坐标不变横坐标变为原来的2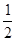 ,得到函数
,得到函数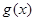 ,求
,求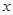 轴的正半轴、直线
轴的正半轴、直线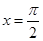 所围成图形的
所围成图形的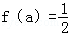 的a的值,并对此时的a值求y的最大值.
的a的值,并对此时的a值求y的最大值. 。
。 的定义域及最小正周期;
的定义域及最小正周期;