题目内容
集合A={（x，y）|x+y=0}，B={（x，y）|x-y=2}，则A∩B是（ ）A．（1，-1）
B．
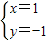
C．{（1，-1）}
D．{1，-1}
【答案】分析：求A∩B，即解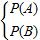
构成的方程组（或不等式组），本题中由集合A、B的条件联立方程组并解方程组，就不难得到答案
解答：解：∵A={（x，y）|x+y=0}，B={（x，y）|x-y=2}，
∴A∩B中的元素满足：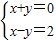
解得：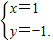
故选C
点评：本题考查的另外一个点是元素的表示方法，由于本题的结果表示含一个点的点集，因此只有C答案才是正确的点集的表示形式．
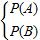构成的方程组（或不等式组），本题中由集合A、B的条件联立方程组并解方程组，就不难得到答案解答：解：∵A={（x，y）|x+y=0}，B={（x，y）|x-y=2}，
∴A∩B中的元素满足：
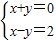
解得：
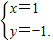
故选C
点评：本题考查的另外一个点是元素的表示方法，由于本题的结果表示含一个点的点集，因此只有C答案才是正确的点集的表示形式．
练习册系列答案
相关题目
设集合A=B={（x，y）|x∈R，y∈R}，从A到B的映射f：（x，y）→（x+2y，2x-y），则在映射f下B中的元素（1，1）对应的A中元素为（ ）
| A、（1，3） | ||||
| B、（1，1） | ||||
C、(
| ||||
D、(
|