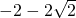Question

已知a²+b²=4，b²+c²=3，c²+a²=3（a，b，c∈R），则ab+bc+ca的最小值为（　　）

• A、-5
• B、-2
• C、2-2

  2

• D、-2-2

  2

Answer 1

分析：根据已知所给的三个等式，变形之后可分别求出a、b、c的值，再把它们的值代入所求代数式，即可得解．

解答：解：联立方程组成方程组，求得a²=2，b²=2，c²=1，
从而a=b=

2

，c=-1时，ab+bc+ca的最小值为-2，
故选B．

点评：本题的关键是让三式相加得到一个等式关系，再分别减去这三个式子，得到a，b，c的值，然后代入即可．