题目内容
在如图的多面体中, ⊥平面
⊥平面 ,
, ,
, ,
, ,
,
 ,
, ,
, ,
, 是
是 的中点.
的中点.

(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: ;
;
【答案】
(Ⅰ)∵ ∴
∴ ∵
∵ ,
, 是
是 的中点∴
的中点∴ ∴
∴ 
∴ 平面
平面 (Ⅱ)∵
(Ⅱ)∵ 平面
平面 ∴
∴ 又
又 ,∴
,∴ 平面
平面
过 作
作 交
交 于
于 ,则
,则 平面
平面 ∴
∴ ∵
∵ ,∴四边形
,∴四边形 平行四边形,∴
平行四边形,∴ ,∴
,∴ ,∴
,∴ ⊥平面
⊥平面 .∴
.∴
【解析】
试题分析:(Ⅰ)证明:∵ ,
,
∴ .
.
又∵ ,
, 是
是 的中点,
的中点,
∴ ,
,
∴四边形 是平行四边形,
是平行四边形,
∴  .
.
∵ 平面
平面 ,
, 平面
平面 ,
,
∴ 平面
平面 .
5分
.
5分
(Ⅱ)证明:∵ 平面
平面 ,
, 平面
平面 ,
,
∴ ,
,
又 ,
, 平面
平面 ,
,
∴ 平面
平面 .
.
过 作
作 交
交 于
于 ,则
,则 平面
平面 .
.
∵ 平面
平面 , ∴
, ∴ .
.
∵ ,∴四边形
,∴四边形 平行四边形,
平行四边形,
∴ ,
,
∴ ,又
,又 ,
,
∴四边形 为正方形,
为正方形,
∴ ,
,
又 平面
平面 ,
, 平面
平面 ,
,
∴ ⊥平面
⊥平面 .
.
∵ 平面
平面 ,
,
∴ .
12分
.
12分
考点:空间线面平行垂直的判定和性质
点评:本题由已知条件可得 两两垂直,依次可建立空间坐标系,利用空间向量求解证明
两两垂直,依次可建立空间坐标系,利用空间向量求解证明

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
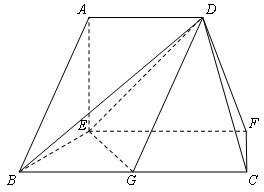 在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点. (2013•泰安二模)在如图的多面体中,AD⊥平面ABE,AE⊥AB,EF∥AD,AD∥BC,AE=AB=BC=EF=2,AD=3
(2013•泰安二模)在如图的多面体中,AD⊥平面ABE,AE⊥AB,EF∥AD,AD∥BC,AE=AB=BC=EF=2,AD=3 在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G 是BC的中点.
在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G 是BC的中点. (2013•济南一模)已知在如图的多面体中,AE⊥底面BEFC,AD∥EF∥BC,BE=AD=EF=
(2013•济南一模)已知在如图的多面体中,AE⊥底面BEFC,AD∥EF∥BC,BE=AD=EF=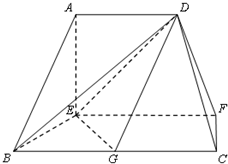 在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.